Hình vuông: Định nghĩa, tính chất và dấu hiệu nhận biết

Trong toán học, hình vuông là một trong những khối hình quan trọng bậc nhất, được dạy xuyên suốt ở các cấp bậc phổ thông. Vì vậy, để ôn lại lý thuyết về hình vuông, ngày hôm nay chúng ta sẽ cùng tìm hiểu tính chất của hình vuông và các vấn đề xoay quanh hình vuông nhé!

Có thể bạn quan tâm

• Bôi kem nghệ qua đêm, nên hay không? Những lưu ý khi sử dụng
• Lịch âm 15/12 – Âm lịch hôm nay 15/12 chính xác nhất – lịch vạn niên 15/12/2023
• Bà bầu có nên ăn hồng xiêm không?
• Top 10 Bài văn viết về an toàn giao thông hay nhất

1. Hình vuông là gì?

Hình vuông ABCD

Bạn đang xem: Hình vuông: Định nghĩa, tính chất và dấu hiệu nhận biết

Trong hình học Euclid, hình vuông là hình tứ giác đều, tức có 4 cạnh bằng nhau và 4 góc bằng nhau (4 góc vuông). Có thể coi hình vuông là hình chữ nhật có các cạnh bằng nhau, hoặc là hình thoi có 2 đường chéo bằng nhau.

Tọa độ Descartes của các đỉnh của một hình vuông có tâm ở gốc hệ tọa độ và mỗi cạnh dài 2 đơn vị, song song với các trục tọa độ là (±1, ±1). Phần trong của hình vuông đó bao gồm tất cả các điểm (x0, x1) với -1 < xi < 1.

Một hình vuông có bốn đỉnh A, B, C, D được kí hiệu lần lượt là ABCD.

2. Các tính chất của hình vuông

Ngoài các tính chất mới, hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi, bao gồm:

• – 2 đường chéo bằng nhau, vuông góc và giao nhau tại trung điểm của mỗi đường.
• – Có 2 cặp cạnh song song.
• – Có 4 cạnh bằng nhau.
• – Có một đường tròn nội tiếp và ngoại tiếp đồng thời tâm của cả hai đường tròn trùng nhau và là giao điểm của hai đường chéo của hình vuông.
• – 1 đường chéo sẽ chia hình vuông thành hai phần có diện tích bằng nhau.
• – Giao điểm của các đường phân giác, trung tuyến, trung trực đều trùng tại một điểm.
• – Có tất cả tính chất của hình chữ nhật, hình thoi và cả hình thang cân.

3. Dấu hiệu nhận biết hình vuông

Một hình tứ giác là một hình vuông nếu như nó thoả mãn một trong những yêu cầu sau:

• – Hình chữ nhật có hai cạnh kề bằng nhau.
• – Hình chữ nhật có hai đường chéo vuông góc.
• – Hình chữ nhật có một đường chéo là phân giác của một góc.
• – Hình thoi có một góc vuông.
• – Hình thoi có hai đường chéo bằng nhau.
• – Hình bình hành có một góc vuông và hai cạnh kề bằng nhau.
• – Hình tứ giác với độ dài các cạnh a, b, c, d mà có diện tích bằng một nửa tổng bình phương 2 cạnh đối diện.

4. Hình nào sau đây là hình vuông?

Có rất nhiều cách để nhận biết đâu là hình vuông. Cách phổ biến nhất đó qua việc chứng minh nó có đầy đủ các dấu hiệu nhận biết. Dưới đây là một số ví dụ và lời giải cho ví dụ đó.

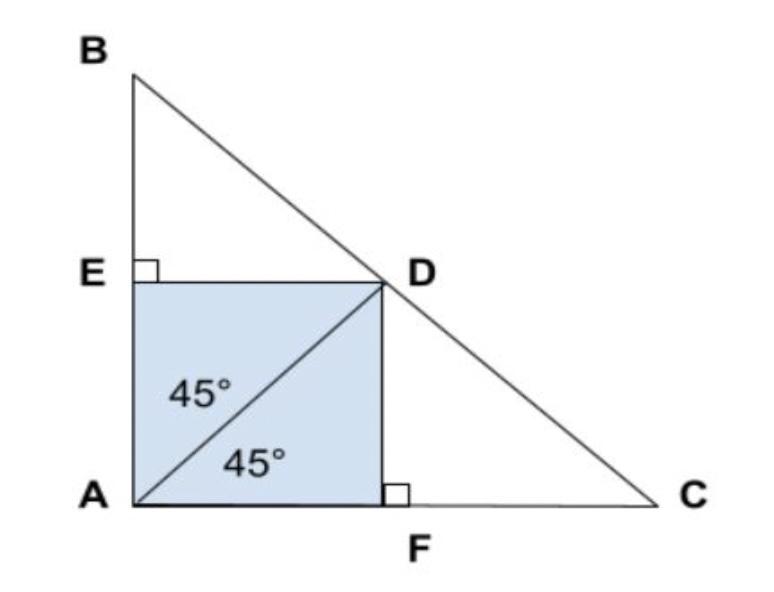
Ví dụ 1: Cho hình sau đây, hỏi tứ giác AEDF là hình gì? Vì sao?

Ta có: EA⊥AF, DF⊥AF (hình vẽ)

⇔ EA // DF (tính chất song song)

Ta có: DE⊥AB, AF⊥AB (hình vẽ)

⇔ DE // AF (tính chất song song)

Xét tứ giác AEDF có EA // DF, DE // AF (cmt)

⇔ Tứ giác AEDF là hình bình hành (định nghĩa)

Xét hình bình hành AEDF có đường chéo AD là phân giác của góc A (∠EAD = ∠DAF = 45°)

⇒ Tứ giác AEDF là hình thoi.

Xét hình thoi AEDF có ∠BAC = ∠EAD + ∠DAF = 45°+45° = 90º

⇒ Tứ giác AEDF là hình vuông.

Ví dụ 2: Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo thứ tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Hỏi tứ giác EKPQ là hình gì? Vì sao?

Ta có: AB = BC = CD = DA (giả thiết)

AE = BK = CP = DQ (giả thiết)

Xem thêm : Ngâm Yến bằng nước nóng hay nước lạnh? Cách làm sạch Yến sào đúng cách nhất

Suy ra: EB = KC = PD = QA

* Xét ΔAEQ và ΔBKE, ta có:

AE = BK (giả thiết)

A = B = 90º

QA = EB (chứng minh trên)

Suy ra: ΔAEQ = ΔBKE (c.g.c) ⇒ EQ = EK (1)

* Xét ΔBKEvà ΔCPK,ta có: BK = CP (giả thiết)

B = C = 90º

EB = KC (chứng minh trên)

Suy ra: ΔBKE = ΔCPK (c.g.c) ⇒ EK = KP (2)

* Xét ΔCPK và ΔDQP, ta có: CP = DQ (giả thiết)

C = D = 90º

DP = CK (chứng minh trên)

Suy ra: ΔCPK = ΔDQP (c.g.c) ⇒ KP = PQ (3)

Từ (1), (2) và (3) suy ra: EK = KP = PQ = EQ

Hay tứ giác EKPQ là hình thoi.

Mặt khác: ΔAEQ = ΔBKE

⇒ ∠(AQE) = ∠(BKE)

Mà ∠(AQE) + ∠(AEQ) = 90º

⇒ ∠(BEK) + ∠(AEQ) = 90º

⇒ ∠(BEK) + ∠(QEK) + ∠(AEQ ) = 180o

Suy ra: ∠(QEK) = 180º – (∠(BEK) + ∠(AEQ)) = 180º – 90º = 90º

Vậy tứ giác EKPQ là hình vuông.

Ví dụ 3: Hình chữ nhật ABCD có AB = 2AD. Gọi P, Q theo thứ tự là trung điểm của AB, CD. Gọi H là giao điểm của AQ và DP, gọi K là giao điểm của CP và BQ. Chứng minh rằng PHQK là hình vuông.

* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD

AP = AB (gt)

QD = 1/2 CD (gt)

Suy ra: AP = QD

Hay tứ giác APQD là hình bình hành.

Lại có: ∠A = 90º

Suy ra tứ giác APQD là hình chữ nhật.

Mà AD = AP = 1/2 AB

Vậy tứ giác APQD là hình vuông.

⇒ AQ ⊥ PD (tính chất hình vuông) ⇒ ∠(PHQ) = 90º (1)

HP = HQ (tính chất hình vuông)

* Xét tứ giác PBCQ, ta có: PB // CD

PB = 1/2 AB (gt)

CQ = 1/2 CD (gt)

Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

∠B = 90º suy ra tứ giác PBCQ là hình chữ nhật

PB = BC (vì cùng bằng AD = 1/2 AB)

Vậy tứ giác PBCQ là hình vuông

⇒ PC ⊥ BC (tính chất hình vuông) ⇒ ∠(PKQ) = 90º (2)

PD là tia phân giác ∠(APQ) (tính chất hình vuông)

PC là tia phân giác ∠(QPB) (tính chất hình vuông)

Suy ra: PD ⊥ PC (tính chất hai góc kề bù) ⇒ ∠(HPK) = 90º (3)

Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.

Trên đây là tính chất của hình vuông và toàn bộ kiến thức xoay quanh hình vuông. Rất mong các em có thể tiếp thu tốt được vấn đề này, và từ đó có thể giải được các bài toán hình khó và trở nên đam mê với bộ môn hình học này nhé!

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp