Đường trung bình của tam giác| Toán 8 chương trình mới
– Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
– Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh đó.
Bạn đang xem: Đường trung bình của tam giác| Toán 8 chương trình mới
– Chú ý: Trong một tam giác, nếu một đường thẳng đi qua trung điểm của một cạnh và song song với cạnh thứ hai thì nó đi qua trung điểm của cạnh thứ ba.
>> Xem thêm: Tổng hợp kiến thức toán 8 chi tiết SGK mới
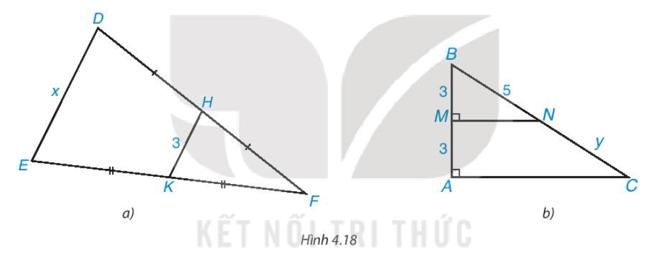
– Hình 4.18a)
Ta có: DH = HF, H ∈ DF nên H là trung điểm của DF;
EK = KF, K ∈ EF nên K là trung điểm của EF.
Xét tam giác DEF có H, K lần lượt là trung điểm của DF, EF nên HK là đường trung bình của tam giác DEF.
Do đó x = 2HK = 2 . 3 = 6.
– Hình 4.18b)
Vì MN ⊥ AB, AC ⊥ AB nên MN // AC.
Mà M là trung điểm của AB (vì AM = BM = 3)
Suy ra MN là đường trung bình của tam giác ABC.
Do đó N là trung điểm của BC nên y = NC = BN = 5.
Vậy x = 6; y = 5.
a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC.
Tứ giác BMNC có MN // BC nên tứ giác BMNC là hình thang (đpcm).
b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.
Tứ giác MNPB có MN // BP (do MN // BC); BM // NP (chứng minh trên).
Do đó, tứ giác MNPB là hình bình hành.
a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.
Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.
Do đó DC // EM (tính chất đường trung bình).
b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).
Mà DI // EM (vì DC // EM).
Do đó DI là đường trung bình của tam giác AEM.
Suy ra I là trung điểm của AM.
Vì ABCD là hình chữ nhật nên và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.
=> AB ⊥ AD; O là trung điểm của AC và BD.
Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của ABD.
=> OH // AD mà AB ⊥ AD nên OH ⊥ AB hay
Tương tự, ta chứng minh được: OK ⊥ AD hay
Ta có
=> Tứ giác AHOK là hình chữ nhật.
a) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN => x = BC = 12.
b) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN => 2x + 3 = 14 => x = 5,5
c) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN => 58 = 2(5x − 1)
=> 58 = 10x – 2 => x = 6
Xét tam giác ABC có:
Xem thêm : Bị thương ăn nước tương có bị sẹo thâm không?
AP = PB = 8 cm
AQ = QC = 7 cm
Khi đó, PQ là đường trung bình tam giác ABC.
Do đó .
Ta có:
Xét ABC có:
P là trung điểm của BC
Q lần lượt là trung điểm của AC
Do đó PQ là đường trung bình ABC.
Khi đó:
Tương tự:
Vậy
a) Xét FBA và FCK ta có:
(hai góc đối đỉnh)
FB = FC (giả thiết)
(AB // CD, hai góc so le trong)
Do đó FBA = ΔFCK (g.c.g)
b) FBA = FCK => FA = FK
Xét ADK có:
EA = ED
FA = FK
=> EF là đường trng bình tam giác ABC.
=> EF // DK
Mà AB // CD nên EF // CD // AB.
c) EF là đường trung bình ADK.
Mà CK = BA (do FBA = FCK)
Xét ABC ta có:
M là trung điểm của AB (gt);
N là trung điểm của AC (gt);
Do đó MN là đường trung bình của ABC nên MN // BC.
=> tứ giác MNPH là hình thang.
Xét ABC ta có:
M là trung điểm của AB (gt);
P là trung điểm của BC;
Do đó MP là đường trung bình của ABC
Vì ACH vuông tại H có HN là trung tuyến (N là trung điểm của AC)
Lại có
Hình thang MNPH (MN // PH) có MP = NH nên là hình thang cân.
Xét ABH có:
AD = BD
BE = EH
Do đó DE là đường trung bình tam giác ABH
Xét ADE có:
B là trung điểm AD
C là trung điểm AE
Do đó BC là đường trung bình của ADE.
Xem thêm : 7 Cách tẩy keo 502 trên quần áo đơn giản và hiệu quả tại nhà
Khi đó DE = 2BC = 2.232 = 464 (m).
Xét ABCvới MN // BC, ta có: (định lí Thalès)
Mà AM = MB (do M là trung điểm của AB) nên AN = NC.
Xét ABCvới MN // BC, ta có: (hệ quả của định lí Thalès)
Mà (do M là trung điềm của AB)
Bài 2 trang 65 SGK toán 8/1 cánh diều
a) Do PN = NB nên N là trung điểm của BP.
Do AM là đường trung tuyến của ∆ABC nên M là trung điểm của BC.
Xét BCP có M, N lần lượt là trung điểm của BC, BP nên MN là đường trung bình của ∆BCP
=> MN // CP.
b) Do AP = PN nên P là trung điểm của AN.
Mà MN // CP, Q ∈ CP nên MN // PQ.
Xét AMN có PQ đi qua P là trung điểm của AN và PQ // MN
=> Q là trung điểm của AM nên AQ = QM.
c) Xét AMN có P, Q lần lượt là trung điểm của AN, AM nên là đường trung bình của AMN.
Lại có MN là đường trung bình của BCP
Khi đó
=> CP = 4PQ.
a) Xét ABC có M, N lần lượt là trung điểm AB, BC nên MN là đường trung bình của ∆ABC
=> MN//AC và (1)
Xét ADC có P, Q lần lượt là trung điểm DC, AD nên PQ là đường trung bình của ADC
=> PQ//AC và (2)
Từ (1) và (2) => MN // PQ; MN = PQ.
Tứ giác MNPQ có MN // PQ; MN = PQ nên MNPQ là hình bình hành.
b) Xét ABD có M, Q lần lượt là trung điểm AB, AD nên MQ là đường trung bình của ABD
=> MQ // BD và
Mà và AC = BD nên MN = MQ.
Hình bình hành MNPQ có MN = MQ nên MNPQ là hình thoi.
c) Ta có MN // AC (câu a), MQ // BD (câu b) và AC ⊥ BD (giả thiết)
Suy ra MN ⊥ MQ hay góc NMQ = 90o
Hình bình hành MNPQ có góc NMQ = 90o nên là hình chữ nhật.
Xét ∆ABH có M, N lần lượt là trung điểm của AB, BH nên MN là đường trung bình ABH.
Suy ra MN//AH (1)
Tương tự, xét ∆AHC ta cũng có PQ là đường trung bình AHC nên PQ//AH (2)
Từ (1) và (2) ta có MN // PQ // AH.
Chứng minh tương tự như trên với ABC và HBC, ta cũng có MQ, NP lần lượt là đường trung bình của ABC và HBC.
Do đó MQ // BC và NP // BC. Suy ra MQ // NP // BC.
Tứ giác MNPQ có MN // PQ và MQ // NP nên MNPQ là hình bình hành.
⦁ Ta có MN//AH và AH ⊥ BC (do H là trực tâm của ∆ABC) nên MN ⊥ BC
Lại có NP // BC nên => MN ⊥ NP hay góc MNP =90°.
Hình bình hành MNPQ có góc MNP =90° nên MNPQ là hình chữ nhật.
Xét ∆ABC có MN là đường trung bình của ∆ABC nên MN=1/2BC
=> BC = 2MN = 2.4,5 = 9(m).
Vậy khoảng cách giữa hai mép dưới của mái khoảng 9 m.
Trên đây là những kiến thức về đường trung bình của tam giác trong chương trình toán 8 kết nối tri thức, chân trời sáng tạo và cánh diều. Bên cạnh đó VUIHOC hướng dẫn các em cách giải các bài tập trong sách giáo khoa. Truy cập vuihoc.vn để cập nhật thêm nhiều kiến thức toán 8 bổ ích nhé các em!
>> Mời bạn tham khảo thêm:
Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp
This post was last modified on 09/04/2024 06:11
Con số may mắn hôm nay 23/11/2024 theo năm sinh: Nhặt TIỀN từ con số…
Tử vi thứ bảy ngày 23/11/2024 của 12 con giáp: Tuổi Thìn chán nản, tuổi…
Vận may của 4 con giáp đang ngày càng xuống dốc. Cuối tuần này (23-24/11),…
Con số cuối cùng trong ngày sinh dự đoán con người sẽ GIÀU CÓ, sống…
Cuối tuần này (23-24/11), 4 con giáp sẽ gặp nhiều may mắn và thành công…
Tử vi hôm nay – Top 3 con giáp thịnh vượng nhất ngày 22/11/2024