Lý thuyết và Các dạng toán về tính chất trực tâm trong tam giác

Tính chất trực tâm là chủ đề quan trọng trong kiến thức Toán học đối với các em học sinh. Vậy trực tâm của một tam giác là gì? Cách chứng minh tính chất trực tâm của tam giác? Tính chất trực tâm trong tam giác nhọn có gì đặc biệt? Các dạng toán liên quan đến trực tâm tam giác?… Trong phạm vi bài viết dưới đây, hãy cùng DINHNGHIA.VN tìm hiểu về chủ đề tính chất trực tâm của tam giác cũng như những nội dung liên quan nhé!

Đường cao của một tam giác là gì?

Đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện được gọi là đường cao của tam giác đó, và mỗi tam giác sẽ có ba đường cao.

Bạn đang xem: Lý thuyết và Các dạng toán về tính chất trực tâm trong tam giác

Xem chi tiết >>> Đường cao là gì? Tính chất và Công thức tính đường cao trong tam giác

Tính chất ba đường cao của tam giác

Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác. Trong hình ảnh bên dưới, S là trực tâm của tam giác LMN.

• Tính chất 1: Trong một tam giác cân thì đường trung trực ứng với cạnh đáy cũng đồng thời là đường phân giác, đường trung tuyến và đường cao của tam giác đó.
• Tính chất 2: Trong một tam giác, nếu như có một đường trung tuyến đồng thời là phân giác thì tam giác đó là tam giác cân.
• Tính chất 3: Trong một tam giác, nếu như có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác cân.
• Tính chất 4: Trực tâm của tam giác nhọn ABC sẽ trùng với tâm đường tròn nội tiếp tam giác tạo bởi ba đỉnh là chân ba đường cao từ các đỉnh A, B, C đến các cạnh BC, AC, AB tương ứng.
• Tính chất 5: Đường cao tam giác ứng với một đỉnh cắt đường tròn ngoại tiếp tại điểm thứ hai sẽ là đối xứng của trực tâm qua cạnh tương ứng.

***Hệ quả: Trong một tam giác đều, trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm nằm trong tam giác và cách đều ba cạnh là bốn điểm trùng nhau.

Trực tâm là gì? Tính chất trực tâm của tam giác

Bài 1: Cho hình sau đây

1. Chứng minh (NS perp LM)
2. Khi (widehat{LNP} = 50^{circ}), hãy tính góc MSP và góc PSQ

Cách giải:

1. Trong (Delta NML) có :

(LP perp MN) nên LP là đường cao

(MQ perp NL) nên MQ là đường cao

mà (PLcap MQ = left { S right })

suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay (NS perp LM)

2. (Delta NMQ) vuông tại Q có:

(widehat{LNP} = 50^{circ}) nên:

(widehat{QMN} = 40^{circ})

(Delta MPS) vuông tại Q có:

(widehat{QMN} = 40^{circ}) nên:

(widehat{MSP} = 50^{circ})

Suy ra

(widehat{PSQ} = 130^{circ}) (kề bù)

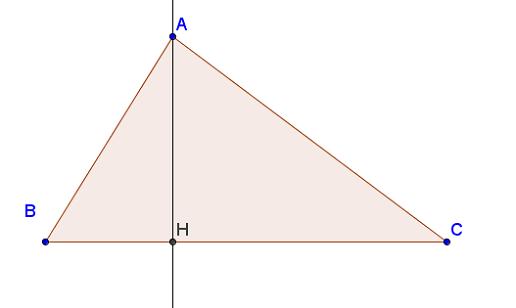
Bài 2: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ta trực tâm của tam giác đó.

Cách giải:

Các đường thẳng HA, HB, HC lần lượt cắt cạnh đối BC, AC, AB tại N, M, E

(Delta HBC) có:

(HN perp BC) nên HN là đường cao

(BE perp HC) nên BE là đường cao

(CM perp BH) nên CM là đường cao

Vậy A là trực tâm của (Delta HBC)

Bài 3: Cho đường tròn (O, R) , gọi BC là dây cung cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.

Cách giải:

Vẽ đường kính (BB_{1})

Vì (AB_{1} parallel HC)

(AH parallel B_{1}C)

(Rightarrow AHCB_{1}) là hình bình hành

(Rightarrow vec{AH} = vec{B_{1}C})

B, C cố định nên (vec{B_{1}C}) không đổi.

Như vậy, (H = T_{vec{B_{1}C}}(A))

Xem thêm : Tổng hợp 21+ cách làm đồ ăn vặt từ bột mì đơn giản mà ai cũng mê

Suy ra tập hợp các điểm H là đường tròn (C’ (O’,R’)), chính là ảnh của đường tròn (C (O,R)) qua phép tịnh tiến (T_{vec{B_{1}C}}).

Bài 4: Cho △ABC có các đường cao AD;BE;CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.

1. Chứng minh: (IJ perp EF)
2. Chứng minh: (IE perp JE)

Cách giải:

1. Sử dụng tính chất đường trung bình trong tam giác vuông ta có:

(FI = frac{1}{2}AH = EI)

(FJ = frac{1}{2}BC = EJ)

Vậy IJ là đường trung trực của EF

(Rightarrow IJperp EF)

2.

Ta có:

(widehat{E_{1}} = widehat{H_{1}} = widehat{ECJ})

(widehat{H_{1}} = widehat{ECJ}) (cùng phụ góc EAH)

Vậy (widehat{E_{1}} = widehat{E_{3}})

(widehat{IEJ} = widehat{E_{1}} + widehat{E_{2}} = widehat{E_{3}} + widehat{E_{2}} = 90^{circ})

(Rightarrow IE perp JE)

Trên đây, DINHNGHIA.VN đã giúp bạn tổng hợp kiến thức về chuyên đề tính chất trực tâm trong tam giác. Hy vọng những kiến thức trên hữu ích với bạn trong quá trình học tập. Nếu có bất cứ câu hỏi nào liên quan đến chủ đề tính chất trực tâm, đừng quên để lại nhận xét bên dưới để chúng mình cùng trao đổi thêm nhé! Nếu hay đừng quên share nha!

Xem chi tiết qua bài giảng dưới đây:

(Nguồn: www.youtube.com)12

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp