Tính chất đường phân giác của tam giác| Toán 8 chương trình mới
– Định lý: Trong một tam giác, đường phân giác cảu một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.
– Chứng minh định lý:
Bạn đang xem: Tính chất đường phân giác của tam giác| Toán 8 chương trình mới
Vẽ đường thẳng qua B song song với AD và cắt AC tại điểm E như hình vẽ.
Theo giả thiết ta có AD là đường phân giác của
=>
Ta có BE // AD =>
=> => cân tại A.
=> AE = AB (1)
Áp dụng định lý thales vào , ta có:
Từ (1) và (2) =>
– Chú ý: Trong ABC, nếu D là điểm thuộc đoạn BC và thỏa mãn thì AD là đường phân giác của góc A.
Cách làm: Áp dụng tính chất đường phân giác của tam giác, các tỉ lệ thức, định lý thales, định lý pytago để biến đổi và tính toán.
Ví dụ: Cho có AB = 5cm, CA = 6cm, BC = 7cm. AE là tia phân giác của . Hãy tính đoạn EC, EB.
Lời giải: Áp dụng tính chất của đường phân giác trong và tính chất của dãy tỉ số bằng nhau ta có:
– Phươn pháp giải: Áp dụng tính chất đường phân giác trong tam giác và lập tỉ lệ thức giữa các đoạn thẳng. Áp dụng kĩ thuật đại số hóa hình học, công thức và kết quả thu được từ công thức tính diện tích tam giác.
– Ví dụ: Cho và các đường phân giác BD và CE. Biết
Hãy tính các cạnh của , biết có chi vi là 45cm.
Lời giải:
Áp dụng tính chất của các đường phân giác BD và CE vào ta có:
Lại có chu vi của là 45 cm, ta có:
AB + BC + CA = 45 = 4t + 6t + 5t = 15t
=> t = 3
Vậy AB = 12cm; BC = 18cm ; CA = 15cm.
>> Xem thêm: Tổng hợp kiến thức toán 8 chi tiết SGK mới
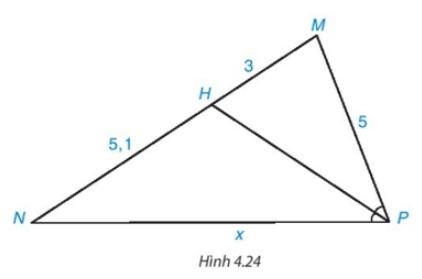
Trong Hình 4.24 có nên PH là tia phân giác của
Áp dụng tính chất đường phân giác của tam giác, ta có:
Theo đề bài, đường phân giác trong của góc A cắt BC tại D nên AD là tia phân giác của
Áp dụng tính chất đường phân giác của tam giác, ta có:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Theo đề bài, ABCD là hình vuông nên AB = AD và AC là tia phân giác của .
Vì M là trung điểm của AB
Vì AC là tia phân giác của hay AI là tia phân giác của , áp dụng tính chất đường phân giác trong ADM, ta có:
Ta có I là điểm gặp nhau nên Mai đi theo quãng đường MI còn Dung đi theo quãng đường DI.
Ta có S = v.t. Mà quãng đường Dung đi gấp 2 lần quãng đường Mai đi, vận tốc của 2 bạn như nhau nên thời gian Dung đi đường sẽ gấp 2 lần thời gian Mai đi đường thì mới gặp nhau tại điểm I.
Dung gặp Mai lúc 7h30p nên thời gian Mai đi trên quãng đường MI là: 7h30 – 7h = 30p
Khi đó thời gian Dung đi là 1h => Thời gian Dung xuất phát từ nhà: 7h30 – 1h = 6h30p.
Vậy dung xuất phát từ lúc 6h30p để gặp Mai lúc 7h30p tại điểm I.
a) Trong ABC, ta có AD là đường phân giác góc A nên ta có
Xem thêm : Các dấu hiệu lừa đảo thông qua ứng dụng Momo
b) Trong EFG, ta có EH là đường phân giác góc E nên ta có
c) Trong t PQR, ta có RS là đường phân giác góc R nên ta có
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
b) Vẽ AH ⊥ BC tại H
a) Trong ABC, ta có: AD là tia phân giác của
Lại có AB = 15 cm; AC = 20 cm.
Xét ABC có DE // AB, theo hệ quả định lí Thalès, ta có:
b) Xét ABC ta có: AB = 15 cm, AC = 20 cm, BC = 25 cm.
Nên BC2 = AB2 + AC2 => ABC vuông tại A.
Khi đó, ta có:
Vậy diện tích ABC là 150 cm2.
c) Kẻ AH ⊥ BC ta có:
Vậy
a) ABC vuông tại A, áp dụng định lí Pythagore, ta có:
BC2 = AC2 + AB2 => BC = 5 cm
AD là tia phân giác góc A nên:
Do đó:
Vậy BC = 5cm ; DB = 15/7 cm; DC = 20/7 cm.
b. Ta có:
Tam giác ABH vuông tại H nên:
Ta có: HD = DB – HB = 15/7 – 9/5 = 12/35 cm.
Vậy AH = 12/5 cm; HD = 12/35 cm;
• Xét ABM có MD là đường phân giác
• Xét ACM có ME là đường phân giác
Mà MB = MC, do đó: , theo định lí Thalès đảo ta có: DE // BC.
Áp dụng tính chất đường phân giác cho ABC, ta có:
AD là đường phân giác của góc BAC
=> 6BD = 4(5 – BD)
<=> 6BD = 20 – 4BD <=> 6BD + 4BD = 20
<=> 10BD = 20 <=> BD = 2.
BE là đường phân giác của góc ABC
=> 4CE = 5(6 – CE)
<=> 4CE = 30 – 5CE <=> 4CE + 5CE = 30
<=> 9CE = 30 <=> CE = 30/9 = 10/3
CF là đường phân giác của góc ACB
=> 5AF = 6(4 – AF) <=> 5AF = 24 – 6AF
<=> 5AF + 6AF = 24 <=> 11AF = 24
<=> AF=24/11
Vậy BD = 2; CE=10/3; AF = 24/11.
Theo tính chất đường phân giác trong tam giác, ta có:
BE là đường phân giác của góc ABC trong ABC
BD là đường phân giác của góc ABM trong ABM
Mà BC = 2BM (do AM là đường trung tuyến của ABC)
Vậy
AD là đường phân giác của góc BAC trong ABC
AE là đường phân giác của góc BAG trong ABG
Vậy
Do ABCD là hình thoi nên AD = AB và AC là đường phân giác của góc BAC.
Xét AMD có AN là đường phân giác góc MAD
Hay (vì AB = 3AM)
Vậy ND = 3MN.
a) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 25 = 52
Suy ra BC = 5.
Do AD là đường phân giác của , theo tính chất đường phân giác trong tam giác, ta có:
Do đó 4DB = 3(5 – DB) <=>4DB = 15 – 3DB
<=> 4DB + 3DB = 15 <=> 7DB = 15 <=> DB = 15/7
Khi đó:
Vậy BC = 5; DB = 15/7 ; DC = 20/7.
b) Kẻ DH ⊥ AC (H ∈ AC).
Suy ra DH // AB (cùng vuông góc với AC)
Áp dụng hệ quả của định lí Thalès trong tam giác ABC với DH // AB, ta có:
Vậy khoảng cách từ điểm D đến đường thẳng AC là DH=12/7.
c) Xét tam giác ABC với DH // AB, ta có:
(hệ quả của định lí Thalès)
Xét tam giác AHD vuông tại H, ta có: AD2 = AH2 + DH2 (định lí Pythagore)
Theo tính chất đường phân giác trong hai tam giác ACD và BCD, ta có:
AE là đường phân giác của góc CAD
BE là đường phân giác của góc CBD
Từ (1) và (2)
Vậy AD.BC = AC.BD.
Trên đây là những kiến thức về tính chất đường phân giác của tam giác lớp 8 trong chương trình toán 8 kết nối tri thức, chân trời sáng tạo và cánh diều. Bên cạnh đó VUIHOC hướng dẫn các em cách giải các bài tập trong sách giáo khoa. Truy cập vuihoc.vn để cập nhật thêm nhiều kiến thức toán 8 bổ ích nhé các em!
>> Mời bạn tham khảo thêm:
Hình thoi và hình vuông
Định lí Thalès trong tam giác
Đường trung bình của tam giác
Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp
This post was last modified on 04/03/2024 23:32
Vận may của 4 con giáp đang ngày càng xuống dốc. Cuối tuần này (23-24/11),…
Con số cuối cùng trong ngày sinh dự đoán con người sẽ GIÀU CÓ, sống…
Cuối tuần này (23-24/11), 4 con giáp sẽ gặp nhiều may mắn và thành công…
Tử vi hôm nay – Top 3 con giáp thịnh vượng nhất ngày 22/11/2024
Con số may mắn hôm nay 22/11/2024 theo năm sinh: Chọn con số ĐẾN LỘC
Tử vi thứ Sáu ngày 22/11/2024 của 12 con giáp: Chó vui vẻ, Hổ may…