“Tính đường cao trong tam giác cân”: Công thức và ứng dụng thực tiễn

Đường cao trong tam giác cân là đoạn thẳng vuông góc kẻ từ đỉnh đến cạnh đáy, đồng thời cũng là đường trung tuyến và phân giác của góc đỉnh. Dưới đây là cách tính chiều cao của tam giác cân thông qua các bước cụ thể và công thức toán học.

• Vẽ đường cao từ đỉnh tam giác cân xuống cạnh đáy.
• Xác định trung điểm của cạnh đáy, đây cũng chính là điểm mà đường cao cắt cạnh đáy.

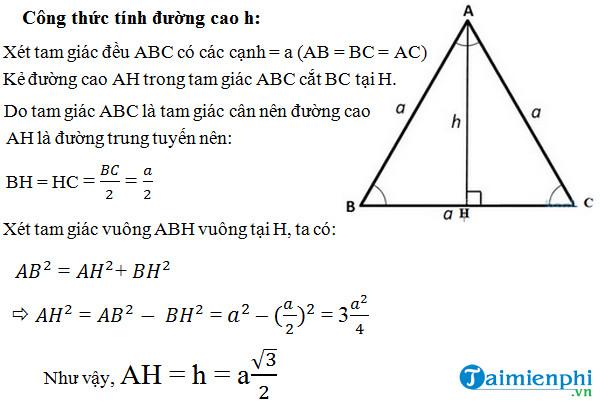
Sử dụng công thức Pythagoras trong tam giác vuông được tạo bởi đường cao, một nửa cạnh đáy và cạnh bên của tam giác cân:

Bạn đang xem: “Tính đường cao trong tam giác cân”: Công thức và ứng dụng thực tiễn

1. Áp dụng công thức $$h^2 = a^2 – left(frac{b}{2}right)^2$$ trong đó:
2. h là chiều cao cần tìm.
3. a là độ dài cạnh bên.
4. b là độ dài cạnh đáy.

Bài tậpCách giảiCho tam giác ABC cân tại A, AB = AC = 4 cm, BC = 14 cmKẻ AH vuông góc với BC tại H.Tính AH: $$AH = sqrt{AB^2 – left(frac{BC}{2}right)^2} = sqrt{4^2 – 7^2} = 3 cm$$Cho tam giác DEF cân tại D, DE = DF = 5 cm, EF = 12 cmKẻ DI vuông góc với EF tại I.Tính DI: $$DI = sqrt{DE^2 – left(frac{EF}{2}right)^2} = sqrt{5^2 – 6^2} = 1 cm$$ Bài tập Cách giải Cho tam giác ABC cân tại A, AB = AC = 4 cm, BC = 14 cm Kẻ AH vuông góc với BC tại H. Tính AH: $$AH = sqrt{AB^2 – left(frac{BC}{2}right)^2} = sqrt{4^2 – 7^2} = 3 cm$$ Cho tam giác ABC cân tại A, AB = AC = 4 cm, BC = 14 cm Kẻ AH vuông góc với BC tại H. Tính AH: $$AH = sqrt{AB^2 – left(frac{BC}{2}right)^2} = sqrt{4^2 – 7^2} = 3 cm$$

Xem thêm : Làn đường là gì?

Kẻ AH vuông góc với BC tại H.

Tính AH: $$AH = sqrt{AB^2 – left(frac{BC}{2}right)^2} = sqrt{4^2 – 7^2} = 3 cm$$

Cho tam giác DEF cân tại D, DE = DF = 5 cm, EF = 12 cm Kẻ DI vuông góc với EF tại I. Tính DI: $$DI = sqrt{DE^2 – left(frac{EF}{2}right)^2} = sqrt{5^2 – 6^2} = 1 cm$$ Cho tam giác DEF cân tại D, DE = DF = 5 cm, EF = 12 cm Kẻ DI vuông góc với EF tại I. Tính DI: $$DI = sqrt{DE^2 – left(frac{EF}{2}right)^2} = sqrt{5^2 – 6^2} = 1 cm$$

Xem thêm :

Kẻ DI vuông góc với EF tại I.

Tính DI: $$DI = sqrt{DE^2 – left(frac{EF}{2}right)^2} = sqrt{5^2 – 6^2} = 1 cm$$

Đường cao trong tam giác cân không chỉ là công cụ để tính chiều cao mà còn giúp xác định diện tích và các tính chất hình học khác của tam giác. Với cách tính và các ví dụ trên, bạn có thể dễ dàng áp dụng để giải quyết các bài toán liên quan đến tam giác cân trong học tập và thi cử.

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp