Nhị thức Newton là một định lý về toán học quan trọng về việc khai triển hàm mũ của tổng, cụ thể là khai triển nhị thức bậc n thành đa thức có n+ 1 số hạng. Nhị thức Newton ứng dụng trong nhiều bài toán chứng minh dãy số và các phép tính tổ hợp chỉnh hợp quan trọng.
Trong bài viết này, VerbaLearn sẽ trình bày tổng quan công thức, cách khai triển, công thức của tam giác Pascal (hệ quả) và ứng dụng vào một số dạng bài tập đặc trưng.
Bạn đang xem: Nhị thức newton: Các công thức và bài tập vận dụng
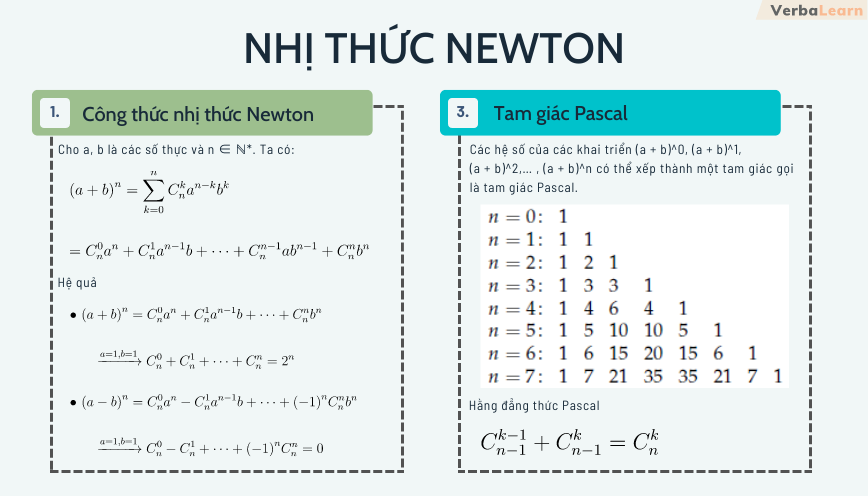
Cho a, b là các số thực và n ∈ ℕ*. Ta có:
Ví dụ 1. Khai triển các nhị thức sau
a) (x + 1)4
b) (x + 2y)5
c)
d)
Hướng dẫn giải
a)
b)
c)
d)
– Trong khai triển (a ± b)n có n + 1 số hạng và các hệ số của các cặp số hạng cách đều số hạng đầu và số hạng cuối thì bằng nhau. Tức là:
– Số hạng tổng quát là và số hạng thứ N thì k = N − 1.
– Trong khai triển (a − b)n thì dấu đan nhau, nghĩa là +, rồi −, rồi +,…
– Số mũ của a giảm dần, số mũ của b tăng dần nhưng tổng số mũ của a và b bằng n.
– Nếu trong khai triển nhị thức Newton, ta gán cho a và b những giá trị đặc biệt thì sẽ thu được những công thức đặc biệt. Chẳng hạn như:
Các hệ số của các khai triển (a + b)0, (a + b)1, (a + b)2,… , (a + b)n có thể xếp thành một tam giác gọi là tam giác Pascal.
Ví dụ: Viết đầy đủ dạng khai triển của các nhị thức sau:
a) (a + b)6
b) (a + b)7
Hướng dẫn giải
a) (a + b)6 = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6.
b) (a + b)7 = a7 + 7a6b + 21a5b2 + 35a4b3 + 35a3b4 + 21a2b5 + 7ab6 + b7.
Bước 1. Viết công thức số hạng tổng quát.
Bước 2. Dùng các tính chất của lũy thừa để rút gọn số hạng tổng quát.
Bước 3. Dựa vào điều kiện cho trước để tìm số hạng thỏa mãn bài toán.
Chú ý:
– Với n ∈ ℕ* và x ≠ 0 thì:
– Với m ∈ ℤ, n ∈ ℕ* và x > 0 thì:
– Với các điều kiện xác định thì:
– Tính chất phân phối của phép nhân đối với phép cộng:
Câu 1. Tìm hệ số của số hạng trong khai triển
a) (2x – 3y)17 chứa x8y9
ĐS:
b) (3x – x2)12 chứa x15
ĐS:
c) chứa x11
ĐS:
d) chứa x2
ĐS:
Hướng dẫn giải
a) Số hạng tổng quát trong khai triển (2x −3y)17 là:
Để có số hạng chứa x8y9 thì: k = 9.
Vậy hệ số của số hạng chứa x8y9 là:
b) Số hạng tổng quát trong khai triển (3x – x2)12 là:
Để có số hạng chứa x15 thì:
12 + k = 15 ⇔ k = 3.
Vậy hệ số của số hạng chứa x15 là
c) Số hạng tổng quát trong khai triển là:
Để có số hạng chứa x11 thì:
20 − 3k = 11 ⇔ k = 3.
Vậy hệ số của số hạng chứa x11 là
d) Số hạng tổng quát trong khai triển là:
Để có số hạng chứa x2 thì:
Vậy hệ số của số hạng chứa x2 là
Câu 2. Tìm hệ số của số hạng chứa x4 trong khai triển (1 + x + 3×2)10.
ĐS: 1695
Hướng dẫn giải
Ta có:
Để có số hạng chứa x4 thì:
Do đó, số hạng chứa x4 là:
Vậy hệ số của số hạng chứa x4 là 1695.
Câu 3. Tìm hệ số của số hạng chứa x10 trong khai triển (1 + x + x2 + x3)5.
ĐS: 101
Hướng dẫn giải
Ta có:
Để có số hạng chứa x10 thì:
Do đó, số hạng chứa x10 là:
Vậy hệ số của số hạng chứa x10 trong khai triển là 101.
Câu 4. Tìm hệ số của số hạng trong khai triển
a) (x + y)25 chứa x12y13
ĐS:
b) (x − 3)9 chứa x4
ĐS:
c) (1 − 3x)11 chứa x6
ĐS:
d) (x2 − 2x)10 chứa x16
ĐS:
e) chứa x31
ĐS:
f) chứa x2
ĐS: -230
Hướng dẫn giải
a) Số hạng tổng quát trong khai triển (x + y)25 là:
Để có số hạng chứa x12y13 thì: k = 13.
Vậy hệ số của số hạng chứa x12y13 là
b) Số hạng tổng quát trong khai triển (x − 3)9 là:
Để có số hạng chứa x4 thì:
9 − k = 4 ⇔ k = 5.
Vậy hệ số của số hạng chứa x4 là
c) Số hạng tổng quát trong khai triển (1 − 3x)11 là:
Để có số hạng chứa x6 thì: k = 6.
Vậy hệ số của số hạng chứa x6 là
d) Số hạng tổng quát trong khai triển (x2 − 2x)10 là
Để có số hạng chứa x16 thì:
24 − k = 16 ⇔ k = 8.
Vậy hệ số của số hạng chứa x16 là
e) Số hạng tổng quát trong khai triển là
Để có số hạng chứa x31 thì:
40 − 3k = 31 ⇔ k = 3.
Vậy hệ số của số hạng chứa x31 là .
f) Ta có:
Để có số hạng chứa x2 thì:
Do đó, số hạng chứa x2 là:
Vậy hệ số của số hạng chứa x2 là −230.
Câu 5. Tìm số hạng không chứa x (độc lập với x) trong khai triển của nhị thức
a) với x ≠ 0
ĐS:
b) với xy ≠ 0
ĐS:
c) với x > 0
ĐS:
Hướng dẫn giải
a) Số hạng tổng quát trong khai triển là:
Để có số hạng không chứa x thì:
18 − 3k = 0 ⇔ k = 6.
Vậy số hạng không chứa x là
b) Số hạng tổng quát trong khai triển
Để có số hạng không chứa x thì:
8 − 2k = 0 ⇔ k = 4.
Vậy số hạng không chứa x là:
c) Số hạng tổng quát trong khai triển là:
Để có số hạng không chứa x thì:
Vậy số hạng không chứa x là
Câu 6. Tìm số hạng chứa x5 trong khai triển:
x(1 − 2x)5 + x2(1 + 3x)10.
Đs: 3310×5
Hướng dẫn giải
Ta có:
Để có số hạng chứa x5 thì
Vậy số hạng chứa x5 là:
Câu 7. Tìm hệ số của số hạng chứa x5 trong khai triển:
(2x + 1)4 + (2x + 1)5 + (2x + 1)6 + (2x + 1)7.
ĐS: 896
Hướng dẫn giải
Ta có:
Để có số hạng chứa x5 thì:
Do đó, số hạng chứa x5 là:
Vậy hệ số của số hạng chứa x5 là 896.
Câu 8. Tìm hệ số của số hạng trong khai triển
a) (2x + y)13 chứa x6y7
ĐS:
b) (x3 – xy)15 chứa x25y10
ĐS:
c) với xy ≥ 0 và y ≠ 0 chứa x6y2
ĐS:
d) (1 + x + 2×2)10 chứa x17
ĐS:
e) (x2 + x – 1)5 chứa x3
ĐS:
f) (1 + x2 − x3)8 chứa x8
ĐS:
g) chứa x8
ĐS:
Câu 9. Tìm số hạng không chứa x (độc lập với x) trong khai triển của nhị thức
a) , với x ≠ 0
ĐS:
b) , với x ≠ 0
ĐS:
c) , với x ≠ 0
ĐS:
d) , với x ≠ 0
ĐS:
e) , với x ≠ 0
ĐS:
f) , với x ≠ 0
ĐS:
g) , với x ≠ 0
ĐS:
h) , với x > 0
ĐS:
i) , với x > 0
ĐS:
j) , với x > 0
ĐS:
k) , với x > 0
ĐS:
– Sử dụng số hạng tổng quát của khai triển là .
– Từ giả thiết tìm ra được giá trị k.
Nhị thức Niu-tơn
– Với a = b = 1, ta có:
– Với a = 1; b = −1, ta có:
– Nếu P(x) = a0 + a1x + a2x2 + ··· + anxn thì tổng các hệ số trong khai triển là P(1).
Câu 1.
a) Tìm số hạng chứa x10 trong khai triển biết
ĐS: −6435×10
b) Tìm số hạng chứa x2 trong khai triển , biết
ĐS: 6×2
c) Tìm số hạng chứa x8 trong khai triển , biết
ĐS: 280×8
Hướng dẫn giải
a) Tìm số hạng chứa x10 trong khai triển biết
Điều kiện n ∈ ℕ, n ≥ 4. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x10 ứng với:
45 − 5k = 10 ⇔ k = 7.
Vậy số hạng chứa x10 trong khai triển là:
b) Tìm số hạng chứa x2 trong khai triển , biết
Điều kiện n ∈ ℕ, n ≥ 2. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x2 ứng với:
12 − 5k = 2 ⇔ k = 2.
Vậy số hạng chứa x2 trong khai triển là:
c) Tìm số hạng chứa x8 trong khai triển , biết
Điều kiện n ∈ ℕ, n ≥ 3. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x8 ứng với:
14 − 2k = 8 ⇔ k = 3.
Vậy số hạng chứa x8 trong khai triển là:
Câu 2. Xác định số nguyên dương n để trong khai triển (1 + x2)n có hệ số của x8 bằng 6 lần hệ số của x4.
ĐS: n = 11
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 4.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Hệ số của x8 là . Hệ số của x4 là
Do hệ số của x8 bằng 6 lần hệ số của x4 nên:
Vậy n = 11 là giá trị cần tìm.
Câu 3.
a) Biết tổng các hệ số trong khai triển (1 + x2)n là 1024. Tìm hệ số của x12.
ĐS: 210
b) Tìm hệ số của x6 trong khai triển với n là số nguyên dương và biết rằng tổng các hệ số trong khai triển bằng 1024.
ĐS: 120
Hướng dẫn giải
a) Biết tổng các hệ số trong khai triển (1 + x2)n là 1024. Tìm hệ số của x12.
Đặt: P(x) = (1 + x2)n.
Tổng các hệ số trong khai triển P(x) là P(1) = 2n.
Do tổng các hệ số trong khai triển (1 + x2)n là 1024 nên:
2n = 1024 ⇔ n = 10.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x12 ứng với:
2k = 12 ⇔ k = 6.
Vậy hệ số của x12 là .
b) Tìm hệ số của x6 trong khai triển với n là số nguyên dương và biết rằng tổng các hệ số trong khai triển bằng 1024.
Đặt .
Tổng các hệ số trong khai triển P(x) là P(1) = 2n.
Do tổng các hệ số trong khai triển là 1024 nên:
2n = 1024 ⇔ n = 10.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x6 ứng với:
2k = 6 ⇔ k = 3.
Vậy hệ số của x6 là .
Câu 4. Cho P(x) = (1 + 2x)n, n ∈ ℕ*. Khai triển P(x) ta được P(x) = a0 + a1x + a2x2 + ··· + anxn. Tính n và a11 biết rằng:
ĐS: 24576
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 11.
Ta có:
Mặt khác:
Khi đó, số hạng tổng quát trong khai triển P(x) là:
Ta suy ra:
Vậy n = 12, a11 = 24576.
Câu 5.
a) Tìm hệ số của x4 trong khai triển , biết .
ĐS: -1792
b) Tìm số hạng không chứa x trong khai triển , biết .
ĐS: 35
c) Tìm số hạng không chứa x trong khai triển , với n ∈ ℕ*, x ≠ 0, biết .
ĐS: 252
d) Tìm hệ số của x10 trong khai triển , biết .
ĐS: 1088640
Hướng dẫn giải
a) Tìm hệ số của x4 trong khai triển , biết .
Điều kiện n ∈ ℕ, n ≥ 2. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x4 ứng với:
4k − 8 = 4 ⇔ k = 3.
Vậy hệ số của x4 trong khai triển là:
b) Tìm số hạng không chứa x trong khai triển , biết .
Điều kiện n ∈ ℕ, n ≥ 3. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng không chứa x ứng với:
Vậy số hạng không chứa x trong khai triển là:
c) Tìm số hạng không chứa x trong khai triển , với n ∈ ℕ*, x ≠ 0, biết .
Điều kiện n ∈ ℕ, n ≥ 1. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng không chứa x ứng với:
8 − 4k = 0 ⇔ k = 2.
Vậy số hạng không chứa x trong khai triển là:
d) Tìm hệ số của x10 trong khai triển , biết .
Điều kiện n ∈ ℕ, n ≥ 2. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x10 ứng với:
30 − 5k = 10 ⇔ k = 4.
Vậy hệ số của x10 trong khai triển là:
Câu 6. Tính biết hệ số của x2 trong khai triển (1 + 3x)n là 90.
ĐS:
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Hệ số của x2 là
Do hệ số của x2 bằng 90 nên:
Vậy:
Câu 7. Trong khai triển nhị thức (1 + 2ax)n,(x ≠ 0) ta có được số hạng đầu là 1, số hạng thứ hai là 48x, số hạng thứ ba là 1008×2. Tìm n và a.
ĐS: n = 8, a = 3
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
– Số hạng đầu là 1 nên .
– Số hạng thứ hai là 48x nên .
– Số hạng thứ ba là 1008×2 nên .
Ta suy ra:
Vậy:
Câu 8. Tìm số hạng không chứa x trong khai triển , biết hiệu hệ số của số hạng thứ ba và thứ hai bằng 35.
ĐS: 252
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
– Hệ số của số hạng thứ ba là .
– Hệ số của số hạng thứ hai là .
Do hiệu hệ số của số hạng thứ ba và thứ hai bằng 35 nên:
Khi đó số hạng không chứa x là .
Câu 9. Cho n là số nguyên dương thỏa mãn điều kiện . Tìm số hạng chứa x10y6 trong khai triển (2×2 + y)n.
ĐS: 14784x10y6
Hướng dẫn giải
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Ta suy ra số hạng chứa x10y6 trong khai triển là:
Câu 10. Cho khai triển nhị thức: (1 − 2x + x3)n = a0 + a1x + a2x2 + ··· + a3nx3n. Xác định n và tìm a6, biết rằng:
ĐS: −31
Hướng dẫn giải
Đặt P(x) = (1 − 2x + x3)n.
Suy ra:
Mặt khác:
Khi đó:
Ta suy ra:
Câu 11. Tìm hệ số của một số hạng hoặc tìm một số hạng
a) Tìm số hạng không chứa x trong khai triển , biết
ĐS: 320320
b) Cho n là số nguyên dương thỏa mãn điều kiện: . Tìm hệ số của x7 trong khai triển: (1 − 2×3)(2 + x)n.
ĐS: −2224
c) Cho n ∈ ℕ* và a, b (b > 0). Biết trong khai triển nhị thức Niu-tơn có hạng tử chứa a4b9, tìm số hạng chứa tích a và b với số mũ bằng nhau.
ĐS: 5005a6b6
d) Cho n là số nguyên dương thỏa mãn . Tìm hệ số của số hạng chứa x11 trong khai triển .
ĐS: 32440320
Hướng dẫn giải
a) Tìm số hạng không chứa x trong khai triển , biết
Điều kiện n ∈ ℕ, n ≥ 9. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng không chứa x ứng với:
Vậy số hạng không chứa x trong khai triển là:
b) Cho n là số nguyên dương thỏa mãn điều kiện: . Tìm hệ số của x7 trong khai triển: (1 − 2×3)(2 + x)n.
Điều kiện n ∈ ℕ, n ≥ 2. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Vậy hệ số của x7 trong khai triển là:
c) Cho n ∈ ℕ* và a, b (b > 0). Biết trong khai triển nhị thức Niu-tơn có hạng tử chứa a4b9, tìm số hạng chứa tích a và b với số mũ bằng nhau.
Điều kiện n ∈ ℕ, n ≥ 4.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Trong khai triển có hạng tử chứa a4b9 nên:
Khi đó số hạng tổng quát là:
Số hạng chứa a và b với số mũ bằng nhau khi:
Vậy số hạng chứa a và b với số mũ bằng nhau là:
d) Cho n là số nguyên dương thỏa mãn . Tìm hệ số của số hạng chứa x11 trong khai triển .
Điều kiện n ∈ ℕ, n ≥ 3. Khi đó:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x11 ứng với:
51 − 5k = 11 ⇔ k = 8.
Vậy hệ số của x11 trong khai triển là:
Câu 12. Trong khai triển nhị thức (1 + ax)n, ta có số hạng đầu bằng 1, số hạng thứ hai bằng 24x, số hạng thứ ba bằng 252×2. Tìm n và a.
ĐS: n = 8, a = 3
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
– Số hạng đầu là 1 nên .
– Số hạng thứ hai là 48x nên .
– Số hạng thứ ba là 252×2 nên .
Ta suy ra:
Vậy:
Câu 13. Biết hệ số của xn−2 trong khai triển (x − 2)n bằng 220. Tìm hệ số của x2.
ĐS: 67584
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Do hệ số của xn−2 trong khai triển bằng 220 nên
Khi đó hệ số của x2 là:
Câu 14. Biết hệ số của xn−2 trong khai triển bằng 31. Tìm số nguyên dương n.
ĐS: n = 32
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Do hệ số của xn−2 trong khai triển bằng 31 nên
Vậy n = 32.
Câu 15. Trong khai triển của nhị thức cho biết tổng hệ số của ba số hạng đầu tiên trong khai triển trên bằng 97. Tìm hệ số của số hạng có chứa x4.
ĐS: 1120
Hướng dẫn giải
Điều kiện n ∈ ℕ, n ≥ 2.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Do tổng hệ số của ba số hạng đầu tiên trong khai triển trên bằng 97 nên:
Khi đó hệ số của x4 trong khai triển là:
Câu 16. Tìm hệ số của một số hạng hoặc tìm một số hạng
a) Biết n nguyên dương thỏa mãn điều kiện . Tìm hệ số của số hạng chứa x8 trong khai triển với x > 0.
ĐS: 14784
b) Biết rằng n là số nguyên dương thỏa . Tìm hệ số của x10 trong khai triển nhị thức (2 + x)n.
ĐS: 1320
c) Tìm hệ số của x10 trong khai triển , biết rằng n là số nguyên dương và tổng các hệ số trong khai triển bằng −2048.
ĐS: −4455
d) Cho n là số nguyên dương thỏa mãn điều kiện: . Tìm hệ số của x7 trong khai triển đa thức (2 − 3x)2n.
ĐS: −2099520
Hướng dẫn giải
a) Biết n nguyên dương thỏa mãn điều kiện . Tìm hệ số của số hạng chứa x8 trong khai triển với x > 0.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x8 trong khai triển ứng với:
Ta suy ra hệ số của x8 trong khai triển là:
b) Biết rằng n là số nguyên dương thỏa . Tìm hệ số của x10 trong khai triển nhị thức (2 + x)n.
Ta có:
Cho a = 3, b = −1 ta được:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Ta suy ra hệ số của x8 trong khai triển là:
c) Tìm hệ số của x10 trong khai triển , biết rằng n là số nguyên dương và tổng các hệ số trong khai triển bằng −2048.
Đặt .
Tổng các hệ số trong khai triển P(x) là P(1) = (−2)n.
Do tổng các hệ số trong khai triển là −2048 nên:
(−2)n = −2048 ⇔ n = 11.
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Số hạng chứa x10 ứng với:
Vậy hệ số của x10 là:
d) Cho n là số nguyên dương thỏa mãn điều kiện: . Tìm hệ số của x7 trong khai triển đa thức (2 − 3x)2n.
Ta có:
Cho a = 1, b = 1 ta được:
Cho a = 1, b = −1 ta được:
Từ (1) và (2) suy ra:
Xem thêm : Salonpas có những dạng nào? Những lưu ý khi sử dụng
Khi đó số hạng tổng quát trong khai triển là:
Ta suy ra hệ số của x7 trong khai triển là:
Ta sử dụng một số công thức như sau:
Câu 1. Chứng minh:
a)
b)
Hướng dẫn giải
a) Xét nhị thức:
Thay x = 1 ta được:
Vậy:
b) Xét nhị thức:
Thay x = 3 ta được:
Lại có:
Vậy:
Câu 2. Tính các tổng sau:
a)
ĐS: S = 32
b)
ĐS:
Hướng dẫn giải
a) Ta có:
b) Xét nhị thức:
Thay x = 2 ta được:
Thay x = −2 ta được:
Trừ hai vế (1) và (2) suy ra:
Vậy:
Câu 3. Tìm số nguyên dương n thỏa mãn các điều kiện sau
a)
ĐS: n = 12.
b)
ĐS: n = 5.
Hướng dẫn giải
a) Ta có:
b) Ta có:
Trừ hai vế ta được:
Câu 4. Chứng minh
a)
b)
Hướng dẫn giải
a) Ta có:
(luôn đúng).
Suy ra điều phải chứng minh.
b) Ta có:
(luôn đúng). Suy ra điều phải chứng minh.
Câu 5. Cho khai triển:
Hãy tìm hệ số lớn nhất trong các số a0, a1, …, a11?
ĐS:
Hướng dẫn giải
Số hạng tổng quát của khai triển là:
Do đó hệ số của số hạng tổng quát là:
Xét:
Suy ra: a0 < a1 < … < a6 < a7
Tương tự:
Suy ra: a8 > a9 > … > a11
Lại có:
Nên: a0 < a1 < … < a6 < a7 = a8 > … > a11
Vậy hệ số lớn nhất là
Câu 6. Chứng minh
a)
b) , ∀n ≥ 2, n ∈ ℕ
Hướng dẫn giải
a) Ta có:
Cộng hai vế (1) và (2) ta được:
Trừ hai vế (1) và (2) ta được:
Vậy:
b) Xét nhị thức:
Trong khai triển trên thì hệ số của xn là (1).
Mặt khác:
Hệ số của xn trong tích trên là:
(2)
Từ (1) và (2) suy ra:
Câu 7. Tính các tổng sau:
a)
ĐS: S = 32010
b)
ĐS: S = 386
Hướng dẫn giải
a) Xét nhị thức:
Thay x = 2 ta được:
Vậy S = 32010.
b) Xét:
Áp dụng công thức , ta có:
Do đó:
Câu 8. Tính các tổng sau:
a)
ĐS: S = 35
b)
ĐS: S = 58
c)
ĐS: S = 22010
d)
ĐS: S = 299
e)
ĐS:
Câu 9. Tìm số nguyên dương n thỏa mãn các điều kiện:
a)
ĐS: n = 11
b)
ĐS: n = 5
c)
ĐS: n = 4
d)
ĐS: n = 10
Câu 10. Chứng minh rằng:
a)
b)
c)
d)
Câu 11. Cho khai triển (1 + 2x)n = a0 + a1x + ··· + anxn, với các hệ số a0, a1, …, an thỏa mãn . Hãy tìm số lớn nhất trong các số a0, a1, …, an?
ĐS:
Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp
Thần Tài ban LỘC trong nháy mắt: 4 con giáp GIÀU nhanh chóng cuối năm…
Top 4 cung hoàng đạo thích làm chủ luôn có tham vọng mở công ty…
Số phận người sinh năm Mão theo cung hoàng đạo: Bạn có thành công không?
Thần Tài mở kho: 4 tuần tới mọi điều ước sẽ thành hiện thực, 4…
Tử vi hôm nay: 4 con giáp có khả năng đạt được thành công vào…
Con số may mắn hôm nay 19/11/2024: Xin số ông DIAH, tận hưởng vận may