Công thức tính diện tích hình bình hành chính xác nhất 2023 và bài tập

Công thức để xác định diện tích hình bình hành là gì? Trong bài viết dưới đây, Hoàng Hà Mobile sẽ cung cấp cho bạn một số công thức và thông tin để có thể tính được diện tích của hình bình hành một cách chính xác. Bên cạnh đó, bài viết sẽ cung cấp cho bạn một số bài tập có đầy đủ lời giải để bạn có thể thực hành.

Tìm hiểu về hình bình hành

Trước khi tìm hiểu về diện tích hình bình hành thì bạn cần phải nắm rõ khái niệm và đặc điểm của loại hình học này. Hình bình hành là hình tứ giác thuộc hình học không gian 2 chiều phẳng. Hình bình hành là tứ giác được tạo từ hai cặp cạnh song song, đối diện và bằng nhau. Đặc biệt, các góc đối diện có số đo bằng nhau. Điểm nổi bật của hình bình hành đó là tứ giác, hai cặp cạnh song song, đối diện và bằng nhau.

Bạn đang xem: Công thức tính diện tích hình bình hành chính xác nhất 2023 và bài tập

Hiện nay, hình bình hành được ứng dụng rất nhiều trong các ngành nghề công việc. Bao gồm ngành kiến trúc, ngành thiết kế, ngành xây dựng và kỹ thuật, công nghệ, khoa học. Hình bình hành được định nghĩa là một trong các khái niệm hình học cơ bản về môn hình học trong bộ môn toán học.

Hình bình hành có thể là hình chữ nhật có 4 cạnh đều vuông góc, là hình thoi có các cạnh của một bằng nhau cùng với các góc đối diện có một độ lớn. Đặc biệt, khái niệm hình bình hành đều là một hình có 4 cạnh bằng nhau với các góc đối diện bằng nhau, cùng độ lớn.

Khái niệm diện tích hình học là gì?

Trước khi tìm hiểu về thuật ngữ diện tích hình bình hành, chúng ta cần hiểu rõ thuật ngữ diện tích hình học. Vậy, diện tích hình học là tất cả diện tích được tính của phần mặt phẳng nằm bên trong hình đó, nghĩa là lượng không gian được bao phủ và thể hiện được tổng thể số đơn vị của không gian chiếm bên trong hình đó.

Các ngành nghề đó bao gồm xây dựng, kiến trúc, ngành thống kê, ngành khoa học và tự nhiên. Ngoài ra, diện tích còn là một khái niệm mang tính cơ bản, là bước đệm cho những khái niệm khác trong lĩnh vực hình học nói riêng và toán học nói chung.

Do đó, việc nắm bắt, hiểu và thực hành các khái niệm về diện tích hình học cực kỳ quan trọng trong lĩnh vực toán học và các ngành nghề liên quan. Thuật ngữ diện tích sẽ giúp xác định, tính toán và đo lường được hình dạng, kích thước khác. Đồng thời, thuật ngữ diện tích hình học sẽ là nền tảng xây dựng các khái niệm về toán học khác. Chính vì vậy, nếu bạn là một người đam mê toán học thì có thể nghiên cứu để áp dụng được thuật ngữ diện tích chính xác vào thực tế.

Khái niệm diện tích hình bình hành là gì?

Dựa vào khái niệm diện tích hình học được phân tích ở trên thì có thể đưa ra kết luận về khái niệm diện tích của hình bình hành. Như vậy, diện tích của hình bình hành là tổng đơn vị của phần mặt phẳng được nhìn thấy bên ngoài so với hình không gian. Thông thường để có thể tính toán và diện tích của hình bình hành cần có được công thức một cách chính xác nhất. Điều này sẽ giúp tránh được tình trạng sai sót khi sử dụng và tính toán. Để tính diện tích của hình bình hành, chúng ta cần xác định được số đo độ dài và số đo chiều rộng của hình.

Tiếp theo, chúng ta sẽ áp dụng công thức tính diện tích của hình bình hành kết hợp cùng các số đo để cho ra kết quả. Đặc biệt, diện tích của hình bình hành cũng được tín với công thức sử dụng đọ dài đường chéo và độ cao của hình.

Lưu ý, khi tính diện tích của hình bình hành, bạn cần phải chú ý đến các đơn vị đo lường cần được sử dụng. Diện tích khi được đo sẽ bằng đơn vị đo độ dài được bình phương như đơn vị mét vuông hoặc đơn vị centimet vuông. Khi lựa chọn sử dụng đơn vị khác thì bạn cần phải đồng nhất đơn vị để đảm bảo được sự chính xác và nhất quán của kết quả.

Công thức xác định diện tích hình bình hành

Diện tích hình bình hành được xác định bằng độ lớn của bề mặt hình, nghĩa là độ lớn phần mặt phẳng chúng ta có thể nhìn thấy bên ngoài.

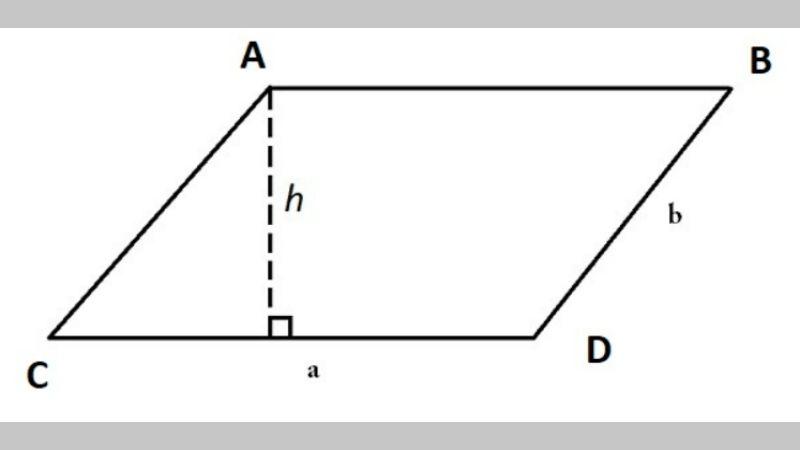
Công thức xác định diện tích của hình bình hành được tính bằng tích của chiều cao nhân với cạnh đáy. Với công thức: S= a x h.

Các yếu tố trong công thức tính diện tích của hình bình hành bao gồm:

• S là diện tích được tính của hình bình hành.
• a là số đo cạnh đáy hình bình hành.
• h là số đo chiều cao, được tính từ đỉnh tới đáy của hình bình hành.

Xem thêm : 7 điều cấm kỵ khi nuôi mèo tránh được phiền phức

Chiều cao thuộc hình bình hành là khoảng cách từ một cạnh của hình đến đường thẳng song song với cạnh đó và đi qua đỉnh của hình. Cạnh đáy của hình bình hành là một trong hai cạnh song song với chiều cao của hình. Khi chúng ta nhân cạnh đáy với chiều cao, chúng ta đang tính tổng diện tích của các hình chữ nhật nhỏ được tạo ra bởi các cạnh của hình bình hành và chiều cao.

Như vậy, công thức cạnh đáy nhân với chiều cao để tính diện tích của hình bình hành là một cách hợp lý và chính xác để tính diện tích của hình này. Ngoài ra, công thức này cũng rất dễ áp dụng trong thực tế.

Một ví dụ để áp dụng công thức: Hình bình hành có cạnh đáy là 7 cm với chiều cao là 9 cm thì diện tích của hình bình hành được xác định với công thức như sau:

Diện tích được tính là: S= a x h= 7 cm x 9 cm= 63 cm2.

Làm thế nào để tính diện tích hình bình hành khi không có số đo chiều cao?

Để tính diện tích của hình bình hành khi không có số đo chiều cao, chúng ta có thể sử dụng một trong các cách sau:

Sử dụng công thức tính diện tích hình bình hành dựa trên đường chéo và một cạnh

Diện tích của hình bình hành bằng ½ tích của đường chéo và một cạnh bất kỳ. Công thức: S= ½ x d x a

Trong đó:

• S được hiểu là diện tích của hình bình hành (đơn vị diện tích)
• d được hiểu là độ dài đường chéo của hình bình hành (đơn vị đo độ dài)
• a được hiểu là độ dài một cạnh bất kỳ của hình bình hành (đơn vị đo độ dài)

Sử dụng công thức tính diện tích hình bình hành dựa trên hai cạnh và một góc

Diện tích của hình bình hành bằng ½ tích của hai cạnh và sin của góc giữa hai cạnh đó.

Công thức: S= ½ x a x b x sin (α)

Trong đó:

• S được định nghĩa là diện tích của hình bình hành (đơn vị diện tích)
• a được định nghĩa là độ dài một cạnh của hình bình hành (đơn vị đo độ dài)
• b được định nghĩa là độ dài cạnh kề với cạnh a (đơn vị đo độ dài)
• α được định nghĩa là góc giữa hai cạnh a và b (đơn vị đo góc)

Áp dụng các tính chất của hình bình hành

Diện tích của hình bình hành bằng diện tích của một hình chữ nhật có cùng độ dài đáy và chiều cao với hình bình hành đó. Hoặc, diện tích của hình bình hành bằng diện tích của một hình thoi có cùng độ dài một cạnh và chiều cao với hình bình hành đó.

Để sử dụng cách này, chúng ta cần biết số đo chính xác độ dài của một cạnh và chiều cao thuộc hình bình hành đó. Sau đó, sử dụng công thức tính diện tích hình chữ nhật hoặc hình thoi để tính diện tích.

Ứng dụng của diện tích hình bình hành trong các lĩnh vực khác

Bên cạnh việc được sử dụng rộng rãi trong toán học, diện tích của hình bình hành được ứng dụng trong các lĩnh vực khác cụ thể như:

• Trong lĩnh vực xây dựng, diện tích của hình bình hành được dùng để có thể xác định được diện tích sàn nhà, mặt bằng ngôi nhà, căn hộ hoặc sân vườn. Việc tính diện tích giúp xác định được các vật liệu xây dựng, vật liệu lót sàn, gạch,…
• Trong lĩnh vực thiết kế nội thất, diện tích của hình bình hành sẽ dùng để xác định được diện tích của không gian để có thể bố trị được đồ nội thật. Việc tính diện tích sẽ giúp tối ưu hóa được không gian và đảm bảo các vật liệu được bố trí một cách hợp lý.
• Đối với lĩnh vực công nghệ, diện tích của hình bình hành sẽ được dùng để hỗ trợ việc thiết kế tấm vi mạch hoặc bố trí các linh kiện khác. Điều này sẽ giúp dễ dàng xác định được không gian cho các phần và loại mạch khác nhau trên bề mặt sản phẩm.
• Đối với lĩnh vực giáo dục và nghiên cứu, diện tích của hình bình hành là một khái niệm hình học cơ bản được ứng dụng trong môn toán học tiểu học và trung học.

Một số dạng bài tập tính diện tích hình bình hành

Sau khi đã nắm được công thức tính diện tích của hình bình hành và ứng dụng của công thức trong các lĩnh vực thì bạn cần phải biết thêm về một số dạng bài tập cơ bản.

• Dạng 1: Tính diện tích của hình bình hành khi có độ dài cạnh đáy và số đo chiều cao. Phương pháp: sử dụng công thức S= a x h để tính diện tích của hình bình hành.
• Dạng 2: Tính độ dài cạnh đáy khi có diện tích của hình và chiều cao. Phương pháp: Sử dụng công thức S= a x h rồi suy ra được công thức tính độ dài của cạnh đáy đó là a = S:h.
• Dạng 3: Tính chiều cao khi có diện tích và số đo độ dài cạnh đáy. Phương pháp: Sử dụng công thức S= a x h rồi suy ra được công thức tính độ dài chiều cao là h= S:a.
• Dạng 4: Mẫu bài tập tổng hợp, đây là dạng bài tập yêu cầu phải có kỹ năng áp dụng kiến thức được học vào thực tế. Khi giải quyết dạng bài tập này, bạn cần phải đọc kỹ nội dung đề bài, xác định được dạng toán có trong bài rồi đưa ra phương án chính xác nhất.

Bài tập diện tích hình bình hành có đáp án chi tiết

Dưới đây là một số bài tập về cách tính diện tích của hình bình hành có đáp án chi tiết mà bạn có thể tham khảo:

Bài 1: Tính diện tích của hình bình hành với độ dài cạnh đáy bằng 7 cm và số đo chiều cao là 5 cm.

Giải:

Áp dụng công thức chuẩn đó là S = a x h => S = 7 cm x 5 cm = 35 cm².

Do đó, diện tích số đo của hình bình hành được tính là 35 cm².

Bài 2: Tính diện tích của hình bình hành với độ dài cạnh đáy bằng 7 cm và số đo chiều cao là 11 cm.

Giải:

Áp dụng công thức chuẩn đó là S = a x h => S = 7 cm x 11 cm = 77 cm²

Do đó, diện tích số đo của hình bình hành được tính là là 77 cm².

Bài 3: Tính diện tích của hình bình hành với độ dài cạnh đáy bằng 6 cm và số đo chiều cao là 5 cm.

Giải:

Áp dụng công thức chuẩn đó là S = a x h => S = 6 cm x 5 cm = 30 cm²

Do đó, diện tích số đo của hình bình hành được tính là là 30 cm².

Tổng kết

Thông qua bài viết trên, bạn đã có thể nắm được công thức tính diện tích hình bình hành một các chính xác và chi tiết nhất. Đồng thời, bạn cũng biết thêm về ứng dụng của công thức tính diện tích của hình bình hành trong toán học và các lĩnh vực khác.

Xem thêm:

• Tính chất của trọng tâm và cách xác định trọng tâm tam giác trong Hình học
• Chu vi hình tròn là gì? Công thức và bài tập vận dụng đầy đủ nhất

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp