Trọng tâm của tam giác là gì? Cách xác định & tính chất trọng tâm của tam giác

Có lẽ một số bạn học sinh đã được nghe về “trọng tâm”. Vậy trọng tâm là gì? Trọng tâm của tam giác xác định như thế nào? Cùng tìm hiểu trong bài học hôm nay nhé.

1. Trọng tâm của tam giác là gì?

Trọng tâm của một hình bất kì là điểm cân bằng của hình đó. Trọng tâm của tam giác cũng vậy, nó là điểm cân bằng của tam giác đó.

Bạn đang xem: Trọng tâm của tam giác là gì? Cách xác định & tính chất trọng tâm của tam giác

Ví dụ chúng ta có một tấm bìa hình tam giác đã xác định được trọng tâm. Khi đặt trọng tâm của tấm bìa hình tam giác lên một đầu kim nhọn thì tấm bìa sẽ được cân bằng, không lệch qua trái hoặc phải.

Vậy làm thế nào để xác định trọng tâm của tam giác, chúng ta xét khái niệm sau.

Khái niệm: Trọng tâm là giao điểm của ba đường trung tuyến trong tam giác.

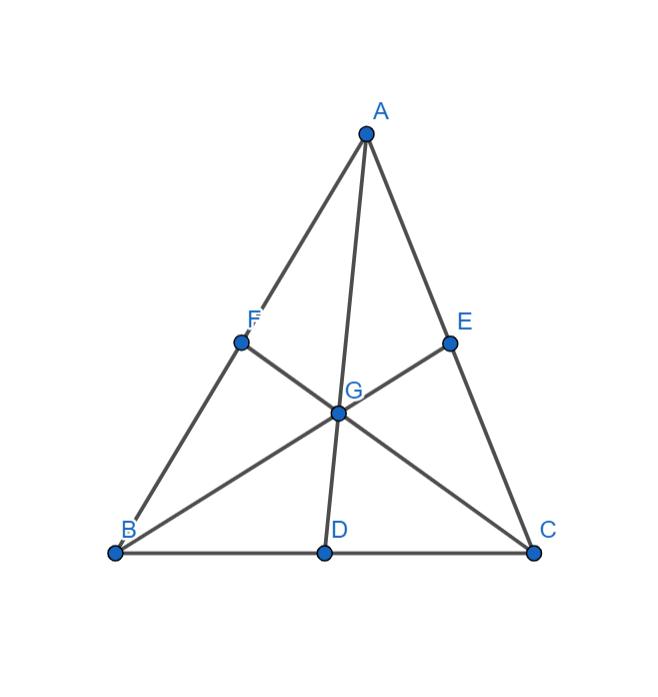
Ví dụ 1:

AD, BE, CF là ba đường trung tuyến của tam giác ABC. AD, BE, CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Ví dụ 2:

HK, IL, JM là ba đường trung tuyến của tam giác HIJ. HK, IL, JM cắt nhau tại N nên N là trọng tâm của tam giác HIJ.

Ví dụ 3:

OS, PR, QT là ba đường trung tuyến của tam giác OPQ. OS, PR, QT cắt nhau tại U nên U là trọng tâm của tam giác OPQ.

1.1. Tính chất trọng tâm của tam giác

Khoảng cách từ trọng tâm đến đỉnh tam giác bằng độ dài đường trung tuyến xuất phát từ đỉnh đó.

Ví dụ 4:

AD, BE, CF là ba đường trung tuyến của tam giác ABC. AD, BE, CF cắt nhau tại G nên G là trọng tâm của tam giác ABC. Ta có:

Vì nên ta suy ra được:

Xem thêm : 5 loại sữa cho mẹ sau sinh giúp gọi sữa về nhanh chóng

Tương tự:

2. Trọng tâm của tam giác vuông

Đối với tam giác vuông, trọng tâm được xác định như đối với tam giác thường: giao điểm của ba đường trung tuyến của tam giác.

Ví dụ 5:

Cho tam giác ABC vuông tại A. AD, CE và BF là ba đường trung tuyến. Như đã nói, trọng tâm tam giác vuông cũng xác định như tam giác thường. Ta thấy trọng tâm G là giao điểm của ba đường trung tuyến AD, CE, BF.

Tính chất của trọng tâm tam giác vẫn được áp dụng đối với tam giác vuông:

Ta có:

Vì nên ta suy ra được:

Xem thêm : 5 loại sữa cho mẹ sau sinh giúp gọi sữa về nhanh chóng

Tương tự:

3. Trọng tâm của tam giác cân

Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh cũng là đường cao của tam giác. Vậy nên trong tam giác cân, trọng tâm vừa nằm trên đường trung tuyến, vừa nằm trên đường cao xuất phát từ đỉnh.

Ví dụ 6:

Cho tam giác ABC cân tại A. AD, CF và BE là ba đường trung tuyến. Vì tam giác ABC cân tại A nên AD cũng là đường cao của tam giác ABC. Ta thấy trọng tâm G nằm trên đường trung tuyến AD và đường cao AD.

Tính chất của trọng tâm tam giác vẫn được áp dụng đối với tam giác cân:

Ta có:

Vì nên ta suy ra được:

Xem thêm : 5 loại sữa cho mẹ sau sinh giúp gọi sữa về nhanh chóng

Tương tự:

4. Trọng tâm của tam giác đều

Trong tam giác đều, mọi đường trung tuyến đều là đường cao và đường phân giác của tam giác đó. Vậy nên trọng tâm tam giác không chỉ là giao điểm của ba đường trung tuyến, trọng tâm tam giác còn có thể là giao điểm của ba đường cao hoặc ba đường phân giác.

Ví dụ 7:

Tam giác ABC là tam giác đều. Ba đường AF, BE, CG vừa là đường trung tuyến, vừa là đường cao và đường phân giác của tam giác đều ABC. H là trọng tâm tam giác, là giao điểm của ba đường trung tuyến vừa là giao điểm của ba đường cao và đường phân giác: AF, BE, CG.

Tính chất của trọng tâm tam giác vẫn được áp dụng đối với tam giác đều:

Ta có:

Vì nên ta suy ra được:

Xem thêm : 5 loại sữa cho mẹ sau sinh giúp gọi sữa về nhanh chóng

Tương tự:

5. Bài tập về trọng tâm của tam giác

Bài 1. Các mệnh đề sau đây đúng hay sai? Tại sao? Nếu sai hãy sửa lại cho đúng

a. Trọng tâm tam giác là giao điểm của ba đường trung tuyến.

b. Trong tam giác cân, trọng tâm vừa là giao điểm của ba đường trung tuyến vừa là giao điểm của ba đường cao.

c. Khoảng cách từ trọng tâm đến đỉnh tam giác bằng độ dài đường trung tuyến xuất phát từ đỉnh đó.

d. Trong tam giác cân, trọng tâm nằm trên đường cao xuất phát từ đỉnh.

e. Trong tam giác đều, có thể xác định trọng tâm bằng cách lấy giao điểm của ba đường cao.

f. Trong tam giác đều, không thể xác định trọng tâm bằng cách lấy giao điểm của ba đường trung tuyến.

g. Trong tam giác đều, có thể xác định trọng tâm bằng cách lấy giao điểm của ba đường trung tuyến, ba đường cao hoặc ba đường phân giác.

ĐÁP ÁN

a.

Đúng. Vì theo như khái niệm đã nêu ở phần 1: Trọng tâm là giao điểm của ba đường trung tuyến trong tam giác.

b.

Sai. Trong tam giác cân, trọng tâm chỉ nằm trên đường trung tuyến và đường cao xuất phát từ đỉnh.

Ta sửa lại như sau: Trong tam giác cân, trọng tâm là giao điểm của ba đường trung tuyến.

c.

Sai. Theo như tính chất của trọng tâm đã nêu ở phần 1: khoảng cách từ trọng tâm đến đỉnh bằng 2/3 độ dài đường trung tuyến.

Ta sửa lại như sau: Khoảng cách từ trọng tâm đến đỉnh tam giác bằng 2/3 độ dài đường trung tuyến xuất phát từ đỉnh đó.

d.

Đúng. Vì trong tam giác cân, đường trung tuyến và đường cao xuất phát từ đỉnh trùng nhau.

e.

Đúng. Vì trọng tâm là giao điểm của ba đường trung tuyến. Mà trong tam giác đều, đường cao cũng là đường trung tuyến.

f.

Sai. Bản chất trọng tâm là giao điểm của ba đường trung tuyến.

Ta sửa lại như sau: Trong tam giác đều, có thể xác định trọng tâm bằng cách lấy giao điểm của ba đường trung tuyến.

g.

Đúng. Vì trọng tâm là giao điểm của ba đường trung tuyến. Mà trong tam giác đều, đường cao cũng là đường phân giác và là đường trung tuyến.

Bài 2. Xem hình bên dưới và cho biết các mệnh đề sau đúng hay sai? Tại sao? Nếu sai hãy sửa lại cho đúng

Cho tam giác ABC vuông tại A. Biết AB = 5, BC = 6, EC = 6.5 và AF, BD, CE là ba đường trung tuyến của tam giác ABC.

a. Đoạn thẳng AC có độ dài xấp xỉ 7.8

b. G là trọng tâm tam giác ABF.

c. G là trọng tâm tam giác ABC.

d. Độ dài đoạn thẳng BG bằng 1/3 độ dài đoạn thẳng BD

e. Đoạn CG có độ dài xấp xỉ 4.3

ĐÁP ÁN

a.

Đúng. Vì ABC là tam giác vuông tại A, nên theo định lý Py – ta – go:

b.

Sai. G chỉ là điểm nằm trên cạnh AF của tam giác ABF.

Ta sửa lại như sau: G không phải là trọng tâm của tam giác ABF.

c.

Đúng. Vì AF, CE, BD là ba đường trung tuyến của tam giác ABC và cắt nhau tại G nên G là trọng tâm tam giác ABC.

d.

Sai. G là trọng tâm tam giác ABC, nên ta áp dụng tính chất của trọng tâm: độ dài từ trọng tâm đến đỉnh bằng 2/3 độ dài đường trung tuyến xuất phát từ đỉnh đó.

Ta sửa lại như sau: độ dài đoạn thẳng BG bằng 2/3 độ dài đoạn thẳng BD.

e.

Đúng. Vì G là trọng tâm tam giác ABC, nên ta áp dụng tính chất của trọng tâm: độ dài từ trọng tâm đến đỉnh bằng 2/3 độ dài đường trung tuyến xuất phát từ đỉnh đó. Ta được:

Câu 3. Một tam giác có bao nhiêu trọng tâm

A. 1

B. 2

C. 3

D. 4

ĐÁP ÁN

A. 1

Câu 4. Trọng tâm tam giác là giao điểm của ba đường:

A. Đường phân giác

B. Đường trung tuyến

C. Đường cao

D. Tất cả đều sai

ĐÁP ÁN

B. Đường trung tuyến

Câu 5. Trong tam giác đều, trọng tâm là giao điểm của ba đường:

A. Đường phân giác

B. Đường trung tuyến

C. Đường cao

D. Tất cả đều đúng

ĐÁP ÁN

D. Tất cả đều đúng

Câu 6. Cho tam giác ABC cân tại A, có AD, BF, CE là các đường trung tuyến, G là trọng tâm của tam giác ABC như hình vẽ. Chứng minh

a.

b.

ĐÁP ÁN

a.

Vì AD là đường trung tuyến và tam giác ABC cân tại A, nên AD cũng là đường cao.

Xét hai tam giác vuông và

chung

(AD là đường trung tuyến)

Suy ra (hai cạnh góc vuông)

b.

Vì nên ta có:

(hai góc tương ứng)

mà (do tam giác ABC cân tại A)

Suy ra

hay (điều phải chứng minh)

Vậy là chúng ta đã hiểu được thế nào là trọng tâm của tam giác, cách xác định trọng tâm của tam giác cũng như tính chất trọng tâm của tam giác. Hy vọng kiến thức trong bài học này có thể giúp ích cho các bạn học sinh trong các bài học tiếp theo.

Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp