Lý thuyết Tập hợp và các phép toán trên tập hợp

a. Tập hợp

+ Mô tả tập hợp:

Bạn đang xem: Lý thuyết Tập hợp và các phép toán trên tập hợp

Cách 1. Liệt kê các phần tử của tập hợp;

Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

+ Quan hệ giữa phần tử và tập hợp:

Phần tử a thuộc tập hợp S hay tập hợp S chứa điểm a: (a in S)

Phần tử a không thuộc tập hợp S hay tập hợp S không chứa điểm a: (a notin S)

+ Số phần tử của tập hợp S: (n(S))

(n(S) = 0 Leftrightarrow S = emptyset ) (S là tập rỗng)

b. Tập hợp con

• Cho hai tập hợp T và S bất kì.

+ T là tập hợp con của S nếu

Kí hiệu: (T subset S)(T là tập hợp con của S) hoặc (S supset T)(S chứa T hoặc T chứa trong S)

Số tập hợp con của tập S có n phần tử là: ({2^n})

+ T không là tập con của S nếu

Xem thêm : Lăng trụ tam giác đều: diện tích, thể tích lăng trụ tam giác đều chuẩn 100%

Kí hiệu: (T notsubset S)

• Quy ước: (emptyset ) và T là tập con của tập hợp T.

c. Hai tập hợp bằng nhau

(S = T) nếu (S subset T) và (T subset S.)

2. Các tập hợp số

a. Mối quan hệ giữa các tập hợp số

Tập hợp các số tự nhiên (mathbb{N} = { 0;1;2;3;4;5;…} )(Kí hiệu (mathbb{N}* = mathbb{N}{rm{backslash }}{ 0} ))

Tập hợp các số nguyên (mathbb{Z} = { …; – 3; – 2; – 1;0;1;2;3;…} ): gồm các số nguyên âm và các số tự nhiên.

Tập hợp các số hữu tỉ (mathbb{Q} = left{ {frac{a}{b}|a,b in mathbb{Z};b ne 0} right})

(Gồm các số nguyên và các số thập phân hữu hạn hoặc vô hạn tuần hoàn)

Tập hợp các số thực(mathbb{R}) gồm các số hữu tỉ và các số vô tỉ.

(Số vô tỉ là các số thập phân vô hạn không tuần hoàn).

Mối quan hệ giữa các tập hợp số: (mathbb{N} subset mathbb{Z} subset mathbb{Q} subset mathbb{R})

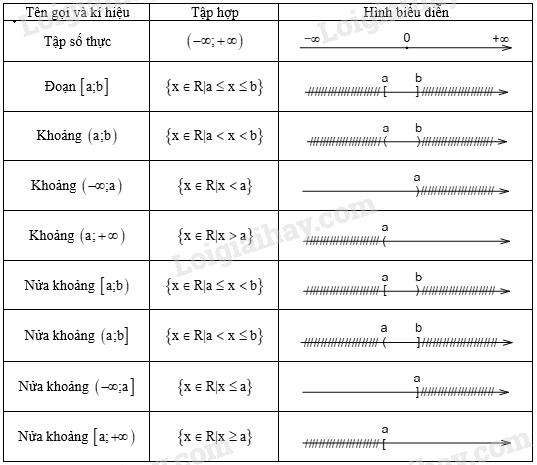
b. Các tập con thường dùng của (mathbb{R})

Xem thêm : Cây xà cừ dùng để làm gì

3. Các phép toán trên tập hợp

a. Giao của hai tập hợp

Giao của hai tập hợp S và T (kí hiệu (S cap T)) là tập hợp gồm các phần tử thuộc cả hai tập hợp S và T.

(S cap T = { x|x in S) và (x in T} .)

b. Hợp của hai tập hợp

Hợp của hai tập hợp S và T (kí hiệu (S cup T)) là tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc T.

(S cup T = { x|x in S) hoặc (x in T} .)

c. Hiệu của hai tập hợp

Hiệu của hai tập hợp S và T (kí hiệu (S{rm{backslash }}T)) là tập hợp gồm các phần tử thuộc S nhưng không thuộc T.

(S{rm{backslash }}T = { x|x in S) và (x notin T} .)

Nếu (T subset S) thì (S{rm{backslash }}T)được gọi là phần bù của T trong S, kí hiệu là ({C_S}T.)

Ví dụ: ({C_mathbb{Z}}mathbb{N} = mathbb{Z}{rm{backslash }}mathbb{N} = { x|x in mathbb{Z}) và (x notin mathbb{N}} = { …; – 3; – 2; – 1} )

Đặc biệt: ({C_S}S = emptyset )

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp