Lý Thuyết Dấu Của Tam Thức Bậc Hai Và Các Dạng Bài Tập

1. Tam thức bậc hai là gì?

Tam thức bậc hai có dạng tổng quát là: f(x) =$ax^{2}+bx+c$.

Trong đó ta có x là biến.

Bạn đang xem: Lý Thuyết Dấu Của Tam Thức Bậc Hai Và Các Dạng Bài Tập

a, b, c là các hệ số, với a≠0.

Ta có nghiệm của tam thức bậc hai là nghiệm của phương trình $ax^{2}+bx+c=0$.

2. Dấu của tam thức bậc hai

2.1. Định lý về dấu của tam thức bậc hai

Hàm số tam thức bậc hai dạng: f(x) =$ax^{2}+bx+c$ (a ≠ 0),

Δ =$b^{2}-4ac$.

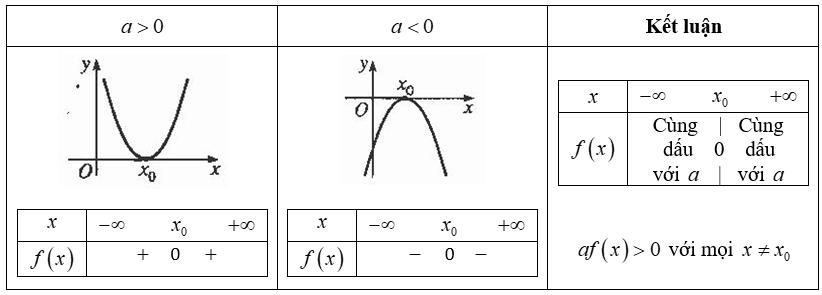
• Nếu Δ < 0 thì f(x) cùng dấu hệ số a, x ∈ R.

• Nếu Δ = 0 thì f(x) có nghiệm kép x = $-frac{b}{2a}$.

• Nếu Δ > 0 thì f(x) có hai nghiệm phân biệt $x_{1}$ và $x_{2}$, cùng dấu với số a khi x < $x_{1}$ hoặc x > $x_{2}$, trái dấu hệ số a nếu $x_{1}$ < x < $x_{2}$.

2.2. Minh họa hình học

Định lý dấu tam thức bậc hai được minh họa bằng hình học như sau:

2.3. Ứng dụng

Ví dụ 1: Cho phương trình $(m^{2}-4)x^{2}+2(m+2)x+1=0$

Tìm m để phương trình có nghiệm.

Giải:

Ví dụ 2: Ta có phương trình $(m^{2}-4)x^{2}+2(m+2)x+1=0$

Để phương trình có nghiệm duy nhất thì m là?

Giải:

Để phương trình có nghiệm duy nhất, ta xét hai trường hợp sau:

3. Định lý thuận của tam thức bậc hai

Chúng ta có định lý thuận về dấu của tam thức bậc 2 là “Trong trái, ngoài cùng”.

Ta có:

Tham khảo ngay bộ tài liệu tổng hợp kiến thức và phương pháp giải mọi dạng bài tập độc quyền của VUIHOC

4. Định lý đảo tam thức bậc hai

Định lý đảo tam thức bậc hai có nội dung như sau:

Cho tam thức bậc hai có dạng là f(x) = $ax^{2}+bx+c (aneq 0)$.

Xem thêm : Vận chuyển hàng hóa bằng đường biển nội địa và lưu ý

f(x) có hai nghiệm phân biệt $x_{1},x_{2}$ và $x_{1}$ < α < $x_{2}$, nếu số α thỏa mãn af(α) < 0

5. Các dạng tam thức bậc hai

5.1. So sánh nghiệm của tam thức với một số cho trước

5.2. So sánh nghiệm của tam thức với hai số cho trước $alpha < beta $

Phương trình có hai nghiệm phân biệt và chỉ một nghiệm thuộc (α;β) khi f(α).f(β) < 0

5.3. Chứng minh phương trình bậc hai có nghiệm

+ Phương trình có hai nghiệm phân biệt nếu có α sao cho af(α) < 0.

+ Phương trình f(x) = 0 có hai nghiệm phân biệt nếu có hai số α, β sao cho f(α).f(β) < 0 và a ≠ 0.

+ Nếu hai số α, β và f(α).f(β) < 0 thì phương trình f(x) = 0 có nghiệm.

5.4. Tìm điều kiện để tam thức bậc hai không đổi dấu trên R

Ta có:

Đăng ký ngay để được thầy cô tổng hợp kiến thức và xây dựng lộ trình ôn tập chuẩn bị sớm cho kì thi tốt nghiệp THPT

6. Các dạng bài tập giải chi tiết dạng dấu của tam thức bậc hai

Bài 1: Xét dấu tam thức bậc hai sau đây: f(x) =$5x^{2}-3x+1$.

Giải:

$Delta =b^{2}-4ac=3^{2}-4.5.1=-11<0$

f(x) cùng dấu với hệ số a

Mà ta có a = 5 > 0

f(x)>0 $forall xin R$

Bài 2: Cho f(x) =$-2x^{2}+3x+5$, xét dấu tam thức bậc hai đã cho.

Giải:

$Delta =b^{2}-4ac=3^{2}-4.(-2).5=49>0$

f(x) có hai nghiệm phân biệt với $x_{1}=-1,x_{2}=frac{5}{2}$

Hệ số a = -2 < 0

Ta có bảng xét dấu:

Nhìn vào bảng xét dấu ta có:

f(x) > 0 khi $xin (-1,frac{5}{2})$

f(x) = 0 khi $x=frac{-b}{2a}-1,x=frac{c}{a}=frac{5}{2}$

f(x) < 0 khi $xin (-infty ,-1)cup (frac{5}{2},+infty )$

Bài 3: Cho bất phương trình $x^{2}-2x+3>0$, hãy giải bất phương trình.

Giải:

Vì bất phương trình gồm một tam thức bậc hai nên ta lập luôn được bảng xét dấu, ta có:

=> Tập nghiệm của bất phương trình là R

Bài 4: Giải bất phương trình sau $x^{2}+9>6x$

Giải:

Ta biến đổi bất phương trình: $x^{2}+9-6x>0$

Bảng xét dấu:

=> Tập nghiệm của bất phương trình là R⟍0

Bài 5: Cho f(x) = $6x^{2}-x-2geq 0$. Hãy giải bất phương trình.

Giải:

Ta có bảng xét dấu vế trái:

<=> Vậy tập nghiệm $x< x_{1}$ hoặc $x>x_{2}$ => S=$(-infty ,-frac{1}{2})cup [frac{2}{3},+infty )$

Bài 6: Cho phương trình f(x) =$(m-2)x^{2}+2(2m-3)x+5m-6=0$

Yêu cầu tìm m để phương trình trên vô nghiệm.

Bài 7: Hãy lập bảng xét dấu của biểu thức cho sau:

f(x) = $(3x^{2}-10x+3)(4x-5)$

Giải:

f(x) có hai nghiệm $x_{1}=frac{1}{3},x_{2}=3$, có hệ số a = 3 > 0 nên mang dấu (+) nếu x <$frac{1}{3}$ hoặc x > 3

Mang dấu (-) nếu $x_{1}<x<x_{2}=frac{1}{3}<x<3$

Nhị thức (4x-5) có nghiệm 4x=5 x = $frac{5}{4}$

Ta có bảng xét dấu:

Từ bảng xét dấu ta kết luận:

f(x)>0 khi $xin (frac{1}{3},frac{5}{4})cup xin (3,+infty )$

f(x)=0 khi $xin S=left { frac{1}{3},frac{5}{4},3 right }$

f(x)<0 khi $xin (-infty ,frac{1}{3})cup (frac{5}{4},3)$

Trên đây là toàn bộ kiến thức và tổng hợp đầy đủ các dạng bài tập về dấu tam thức bậc hai. Hy vọng rằng sau khi đọc bài viết, các bạn học sinh có thể áp dụng công thức để giải các bài tập một cách dễ dàng. Để học và ôn tập kiến thức lớp 12 ôn thi Toán THPT Quốc gia, hãy truy cập Vuihoc.vn và đăng ký khóa học ngay từ hôm nay nhé!

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp