Lý thuyết Bội chung. Bội chung nhỏ nhất Toán 6 KNTT với cuộc sống

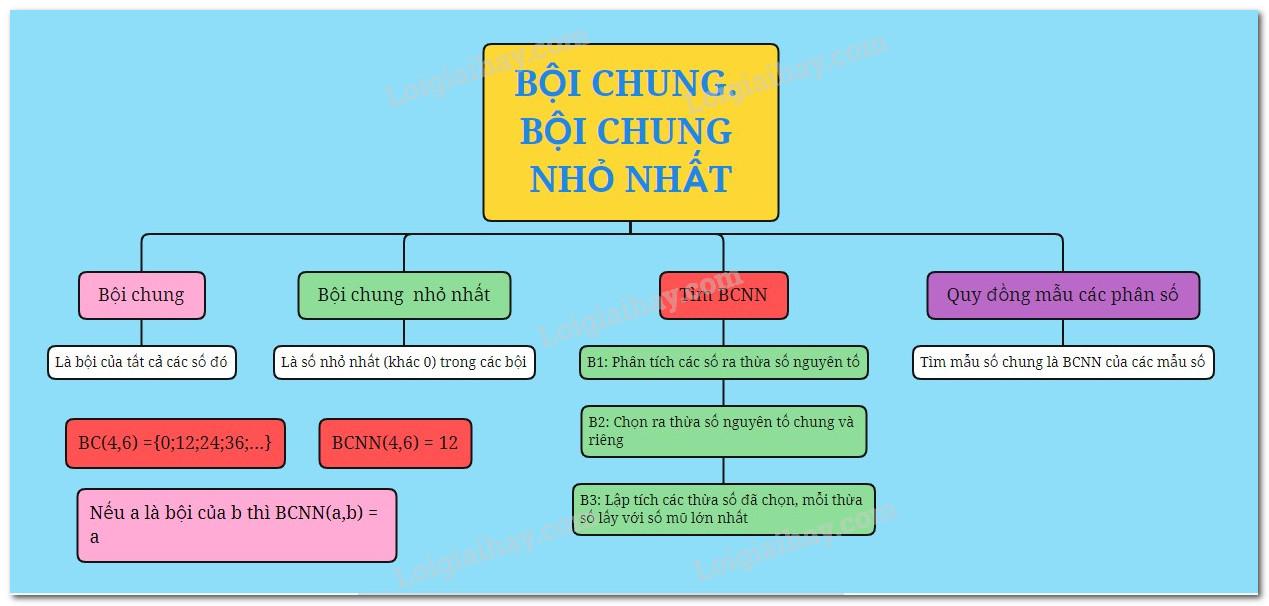
BỘI CHUNG. BỘI CHUNG NHỎ NHẤT

I. Bội chung

Bạn đang xem: Lý thuyết Bội chung. Bội chung nhỏ nhất Toán 6 KNTT với cuộc sống

1. Định nghĩa

Bội chung của hai hay nhiều số là bội của tất cả các số đó.

2. Kí hiệu

+ BC(left( {a;b} right)) là tập hợp các bội chung của (a) và (b).

3. Cách tìm bội chung

a) Tìm bội chung của hai số a và b

Bước 1: Viết tập hợp các bội B(a) của a và các bội B(b) của b.

Bước 2: Tìm những phần tử chung của B(a) và B(b).

Ví dụ: (Bleft( 3 right) = left{ {0;3;6;9;12;…} right}); (Bleft( 2 right) = left{ {0;2;4;6;8;10;12;…} right})

Nên (BCleft( {2;3} right) = left{ {0;6;12;…} right})

b) Tìm bội chung của ba số a, b và c

Bước 1: Viết tập hợp các bội của a, của b và của c: B(a), B(b), B(c)

Bước 2: Tìm những phần tử chung của B(a), B(b) và B(c).

Nhận xét:

+) (x in BCleft( {a,b} right)) nếu (x vdots a) và (x vdots b)

+) (x in BCleft( {a,b,c} right)) nếu (x vdots a); (x vdots b) và (x vdots c)

Chú ý:

+ Ta chỉ xét bội chung của các số khác 0.

+ Giao của hai tập hợp là một tập hợp gồm các phần tử chung của hai tập hợp đó.

+ Kí hiệu: Giao của tập hợp A và tập hợp B là (A cap B)

Ví dụ:(Bleft( 2 right) cap Bleft( 3 right) = BCleft( {2,3} right))

II. Bội chung nhỏ nhất

1. Định nghĩa

Xem thêm : Bầu ăn hàu được không? Nên ăn thế nào khi mang thai?

Bội chung nhỏ nhất (BCNN) của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó..

2. Kí hiệu

+) (BCNNleft( {a,b} right)) là bội chung nhỏ nhất của (a) và (b).

+) BC(left( {a,b} right)) là tập hợp còn BCNN(left( {a,b} right)) là một số.

3. Cách tìm bội chung lớn nhất bằng định nghĩa

a) Cách tìm bội chung nhỏ nhất trong các trường hợp đặc biệt

Nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho là số lớn nhất đó.

Nếu (a vdots b) thì (BCNNleft( {a,b} right) = a)

Với mọi số tự nhiên a và b ta có:

(BCNNleft( {a,1} right) = a;)(BCNNleft( {a,b,1} right) = BCNNleft( {a,b} right))

Ví dụ:

Bội chung nhỏ nhất của 12 và 36 là 36 vì (36 vdots 12).

b) Cách tìm BCNN của hai số a và b bằng định nghĩa

Bước 1. Tìm tập hợp các bội chung của hai số a và b: BC(left( {a,b} right))

Bước 2. Tìm số nhỏ nhất khác 0 trong các bội chung vừa tìm được: BCNN(left( {a,b} right))

Ví dụ : Tìm BCNN (15, 20)

(begin{array}{l}Bleft( {15} right) = left{ {0;15;30;45;60;.75;90;105;120;..} right}Bleft( {20} right) = left{ {0;20;40;60;80;100;120;…} right}BCleft( {15,20} right) = left{ {0;60;120;…} right}end{array})

Số nhỏ nhất khác 0 trong các bội chung trên là 60 nên BCNN (15, 20)=60.

III. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố

1. Cách tìm bội chung nhỏ nhất-BCNN

Ví dụ: Tìm BCNN của (15) và (20.)

Ta có (15 = 3.5;20 = {2^2}.5)

Nên (BCNNleft( {15,20} right) = {2^2}.3.5 = 60.)

2. Cách tìm bội chung thông qua bội chung nhỏ nhất

Để tìm bội chung của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.

Ví dụ: (BCNNleft( {15, 20} right) = 60) nên (BCleft( {15, 20} right) = Bleft( {60} right) = left{ {0;60;120;…} right})

IV. Ứng dụng trong quy đồng mẫu các phân số

Xem thêm : Tác động đến sự sống của nhân loại – Mối quan hệ giữa con người và môi trường

Tìm mẫu chung của hai phân số

Ví dụ:Quy đồng mẫu số hai phân số (dfrac{7}{{30}}) và (dfrac{5}{{42}})

(begin{array}{l}30 = 2.3.542 = 2.3.7end{array})

(begin{array}{l} Rightarrow BCNNleft( {30;42} right) = 2.3.5.7 = 210 Rightarrow BCleft( {30,42} right) = left{ {0;210;420;…} right}end{array})

+) Cách 1: Chọn mẫu chung là 210. Ta được:

(begin{array}{l}dfrac{7}{{30}} = dfrac{{7.7}}{{210}} = dfrac{{49}}{{210}}dfrac{5}{{42}} = dfrac{{5.5}}{{42.5}} = dfrac{{25}}{{210}}end{array})

+) Cách 2: Chọn mẫu chung là một bội chung bất kì khác 0 của 30 và 42. Chẳng hạn 420, ta được:

(begin{array}{l}dfrac{7}{{30}} = dfrac{{7.14}}{{30.14}} = dfrac{{98}}{{420}}dfrac{5}{{42}} = dfrac{{5.10}}{{42.10}} = dfrac{{50}}{{420}}end{array})

CÁC DẠNG TOÁN VỀ BỘI CHUNG. BỘI CHUNG NHỎ NHẤT

I. Nhận biết và viết tập hợp các bội chung của hai hay nhiều số

Phương pháp:

+ Để nhận biết một số là bội chung của hai số, ta kiểm tra xem số này có chia hết cho hai số đó hay không?

+ Để viết tập hợp các bội chung của hai hay nhiều số, ta viết tập hợp các bội của mỗi số rồi tìm giao của các tập hợp đó.

II. Bài toán đưa về việc tìm BC, BCNN của hai hay nhiều số

Phương pháp:

Phân tích đề bài, suy luận để đưa về việc tìm BC, BCNN của hai hay nhiều số.

Ví dụ:

Có hai chiếc máy bay A và B. Lịch bảo dưỡng định kì đối với máy A là 6 tháng và đối với máy B là 9 tháng. Hai máy vừa cùng được bảo dưỡng vào tháng 5. Hỏi sau ít nhất bao nhiêu tháng nữa thì hai máy lại được bảo dưỡng trong cùng một tháng.

Giải

Thời gian hai máy bay được bảo dưỡng cùng nhau trong lần tiếp theo là BCNN của 6 và 9.

Ta có: BCNN(6, 9)= 18

Vậy sau ít nhất 18 tháng thì hai máy bay lại được bảo dưỡng trong cùng một tháng.

III. Tìm các bội chung của hai hay nhiều số thỏa mãn điều kiện cho trước

Phương pháp:

+ Tìm BCNN của hai hay nhiều số cho trước.

+ Tìm các bội của BCNN.

+ Chọn trong số đó các ước hoặc các bội thỏa mãn điều kiện đã cho.

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp