Chứng minh 3 điểm thẳng hàng bằng vectơ lớp 10

Bài toán chứng minh 3 điểm thẳng hàng bằng vectơ trong chương trình lớp 10 các bạn sẽ gặp rất nhiều. Đặc biệt là các em lại mới tiếp xúc với kiến thức về vectơ nên sẽ gặp nhiều khó khăn. Vì vậy hôm nay thầy muốn gửi tới các em phương pháp chứng minh ba điểm thẳng hàng.

Trước thầy cũng có một bài giảng viết về chủ đề này rồi nhưng với tiêu đề là “Chứng minh hai vectơ cùng phương“. Bản chất nó vẫn giống với bài viết hôm nay nhưng thầy vẫn muốn viết thêm bài giảng này nữa. Các bạn có thể xem thêm bài giảng trên.

Bạn đang xem: Chứng minh 3 điểm thẳng hàng bằng vectơ lớp 10

Phương pháp chứng minh ba điểm thẳng hàng

Ba điểm A, B, C được gọi là thẳng hàng nêú chúng cùng nằm trên một đường thẳng hay có một đường thẳng đi qua 3 điểm này. Từ cơ sở này chúng ta sẽ đưa bài toán trên về việc chứng minh 2 vectơ cùng phương.

Với 3 điểm A, B, C cùng nằm trên một đường thẳng giả sử là d thì ta sẽ có được 3 đoạn thẳng là: AB, BC và AC. Từ đây ta sẽ xác định được các vectơ là: $vec{AB}, vec{BA}, vec{AC}, vec{CA}, vec{BC}, vec{CB}$. Tất cả các vectơ trên đều cùng phương. Nếu bạn nào chưa rõ những khái niệm như: Hai vectơ cùng phương, hai vec tơ cùng hướng, hai vectơ bằng nhau thì hãy xem bài giảng này của thầy nhé: Các khái niệm cơ bản của vectơ cực dễ hiểu

Từ phân tích ở trên chúng ta sẽ đi tới một kết luận:

Để chứng minh 3 điểm A, B, C thẳng hàng ta sẽ đi chứng minh các vectơ cùng phương. Cụ thể là $vec{AB}=kvec{AC}$ hoặc $vec{AB}=kvec{BC}$ hoặc $vec{AC}=kvec{BC}$… Các bạn có thể chọn bất kì 2 cặp vectơ nào trong 6 vectơ thầy nêu ở trên để chứng minh.

Việc chứng minh vectơ nọ bằng k lần vectơ kia có thể chứng minh trực tiếp cũng có thể phải chứng minh gián tiếp. Tức là phải thông qua những vectơ trung gian nào đó.

Thầy muốn nói thêm 1 chút chỗ này nữa để nhiều bạn chưa rõ các xác định một điểm nằm ở đâu khi giả thiết cho 1 đẳng thức vectơ.

Nếu giả thiết cho $vec{MB}=2vec{MC}$ có nghĩa là đoạn MB=2MC và $vec{MB}$ cùng hướng với $vec{MC}$, tức là B và C nằm về 1 phía so với điểm M. Do đó trên cạnh BC các bạn kéo dài về phía C lấy điểm M sao cho MB=2MC.

Nếu giả thiết cho $vec{NA}=-2vec{NC}$ có nghĩa là đoạn NA=2NC và $vec{NA}$ ngược hướng với $vec{NC}$, tức là điểm N nằm giữa 2 điểm A và C. Do đó trên đoạn AC các bạn lấy điểm N sao cho NA=2NC.

Phương pháp như vậy là rõ ràng rồi phải không các bạn, giờ chúng ta sẽ cùng tìm hiểu một vài ví dụ xem như thế nào nhé.

Bài tập chứng minh 3 điểm thẳng hàng bằng vectơ

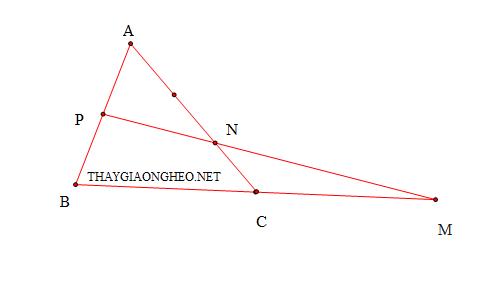
Bài tập 1: Cho tam giác ABC có P là trung điểm của AB và hai điểm M, N thỏa các hệ thức: $vec{MB}-2vec{MC}=vec{0}$ và $vec{NA}+2vec{NC}=vec{0}$. Chứng minh rằng 3 điểm M, N, P thẳng hàng.

Hướng dẫn:

Như phân tích ở phần phương pháp thì với bài toán này để chứng minh ba điểm M, N, P thẳng hàng các em cần chứng minh 2 cặp véctơ bất kì trong những vectơ sau cùng phương: $vec{MN}, vec{NM}, vec{MP}, vec{PM}, vec{NP}, vec{PN}$.

Ở đây thầy sẽ chọn ra 2 cặp vectơ và chứng minh chúng cùng phương theo 2 cách với mục đích giúp các e hiểu sâu hơn cách làm.

Xem thêm : Vượt Trung Quốc, Ấn Độ trở thành nước đông dân nhất thế giới

Cách thứ 1: Thầy sẽ đi chứng minh: $vec{MN}=kvec{MP}$

Cách thứ 2: Thầy sẽ đi chứng minh $vec{PN}=kvec{PM}$

Với cả 2 cách chứng minh này thầy sẽ đưa các vectơ trên về các vectơ trung gian khác là: $vec{AB}, vec{BC}, vec{CA}$

Cách thứ 1: Biến đổi 2 vectơ $vec{MN}, vec{MP}$ theo 2 vectơ $vec{CB}, vec{CA}$

Xét:

$vec{MN}=vec{MC}+vec{CN}=vec{CB}+frac{1}{3}vec{CA}$

$Rightarrow 3vec{MN}=3vec{CB}+vec{CA}$ (1)

Xét:

$vec{MP}=vec{MB}+vec{BP}=2vec{CB}+frac{1}{2}vec{BA}$

$=2vec{CB}+frac{1}{2}(vec{CA}-vec{CB})=2vec{CB}+frac{1}{2}vec{CA}-frac{1}{2}vec{CB}$

$=frac{3}{2}vec{CB}+frac{1}{2}vec{CA}$

$Rightarrow 2vec{MP}=3vec{CB}+vec{CA}$ (2)

Từ (1) và (2) ta có: $3vec{MN}=2vec{MP} Leftrightarrow vec{MN}=frac{2}{3}vec{MP}$

Từ đây ta có: $ vec{MN}$ cùng phương với $vec{MP}$

Xem thêm : CỔNG GIAO DỊCH BẢO HIỂM XÃ HỘI ĐIỆN TỬ

Do đó 3 điểm M, N, P thẳng hàng (đpcm)

Cách 2: Biến đổi 2 vectơ $vec{PN}, vec{PM}$ theo 2 vectơ $vec{AC}, vec{AB}$

Xét:

$vec{PN}=vec{AN}-vec{AP}=frac{2}{3}vec{AC}-frac{1}{2}vec{AB}$

$Rightarrow 6vec{PN}=4vec{AC}-3vec{AB}$ (3)

Xét:

$vec{PM}=vec{PB}+vec{BM}=frac{1}{2}vec{AB}+2vec{BC}$

$=frac{1}{2}vec{AB}+2(vec{AC}-vec{AB})=frac{1}{2}vec{AB}+2vec{AC}-2vec{AB}$

$=2vec{AC}-frac{3}{2}vec{AB}$

$Rightarrow 2vec{PM}=4vec{AC}-3vec{AB}$ (4)

Từ (3) và (4) ta có: $6vec{PN}=2vec{PM} Leftrightarrow vec{PN}=frac{1}{3}vec{PM}$

Từ đây ta có: $ vec{PN}$ cùng phương với $vec{PM}$

Xem thêm : CỔNG GIAO DỊCH BẢO HIỂM XÃ HỘI ĐIỆN TỬ

Do đó 3 điểm M, N, P thẳng hàng (đpcm)

Lời kết

Đọc tới đây rồi thì thầy hy vọng tất cả các bạn sẽ hiểu và làm được những bài toán chứng minh ba điểm thẳng hàng bằng vectơ như thế này. Thầy đã cố gắng diễn đạt sao cho các bạn dễ hiểu và tiếp thu nhất nhưng chắc không tránh khỏi những sai sót. Vì vậy thầy hy vọng nhận được những góp ý từ các bạn để thầy có thể hoàn thiện bài giảng hơn nữa. Nếu có phương pháp nào hay nữa xin hãy chia sẻ dưới khung bình luận của bài giảng này để chúng ta làm phong phú hơn hướng đi.

Các bạn có thể xem thêm bài giảng về chủ đề này trong link thầy đặt phía bên trên đầu bài viết nhé.

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp