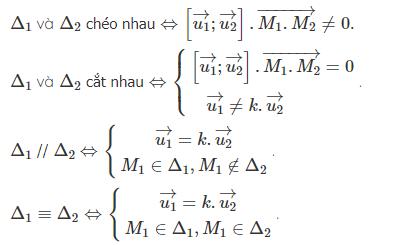
Phương Trình Đường Thẳng Trong Không Gian: Lý Thuyết Và Bài Tập

1. Lý thuyết phương trình đường thẳng trong không gian

1.1. Phương trình tham số của đường thẳng trong không gian

Đường thẳng d đi qua $M_{0}(x_{0}; y_{0}; z_{0})$ và vectơ chỉ phương $overrightarrow{u}=(a; b; c)$

Phương trình tham số d:

Bạn đang xem: Phương Trình Đường Thẳng Trong Không Gian: Lý Thuyết Và Bài Tập

$x = x_{0} + at$

$y = y_{0} + bt$

$z = z_{0} + ct$

$(t epsilon R)$

1.2. Phương trình chính tắc của đường thẳng trong không gian

Đường thẳng d đi qua $M_{0}(x_{0};y_{0};z_{0})$ và vectơ chỉ phương $overrightarrow{u} = (a; b; c)$

Phương trình chính tắc của d: $frac{x – x_{0}}{a} = frac{y – y_{0}}{b} = frac{z – z_{0}}{c} (abc neq 0)$

1.3. Vị trí tương đối của 2 đường thẳng

Trong không gian cho 2 đường thẳng 1 đi qua $M_{1}$ và có một vecto chỉ phương $overrightarrow{u}$. Khi đó vị trí tương đối $Delta_{1}$ và $Delta_{2}$ được xác định như sau:

1.4. Vị trí tương đối của đường thẳng với mặt phẳng

Đường thẳng d đi qua $M_{0}(x_{0};y_{0};z_{0})$ và có vectơ chỉ phương $overrightarrow{u} = (a; b; c)$ và mặt phẳng (P): $Ax + By + Cz + D = 0$ có vecto pháp tuyến $overrightarrow{u} = (A; B; C)$. Khi đó:

1.5. Góc giữa 2 đường thẳng

Trong không gian cho 2 đường thẳng $Delta_{1}$ có một vecto chỉ phương $overrightarrow{u_{1}} = (a_{1}; b_{1}; c_{1})$ khi đó:

>> Xem thêm: Góc giữa 2 mặt phẳng: Định nghĩa, cách xác định và bài tập

1.6. Góc giữa đường thẳng và mặt phẳng

Trong không gian cho đường thẳng $Delta$ có vecto chỉ phương $overrightarrow{u_{1}} = (a; b; c)$ mặt phẳng (P) có vecto chỉ phương $overrightarrow{n} = (A; B; C)$. Khi đó:

>> Xem thêm: Cách xác định góc giữa đường thẳng và mặt phẳng trong không gian

1.7. Khoảng cách từ 1 điểm tới 1 đường thẳng

Cho điểm M cùng đường thẳng $Delta$ đi qua N có vectơ $overrightarrow{u}$. Khi đó khoảng cách từ điểm M đến $Delta$ xác định bởi công thức.

1.8. Khoảng cách giữa 2 đường thẳng chéo nhau

Cách 1:

Trong không gian cho đường thẳng $Delta_{1}$ đi qua $M_{1}$ có vecto chỉ phương $overrightarrow{u_{1}} . Delta_{2}$ đi qua $M_{2}$ có vecto chỉ phương $overrightarrow{u_{2}}$. Khi đó:

Cách 2:

Gọi AB là đoạn thẳng vuông góc $Delta_{1}, Delta_{2}$ với $A epsilon Delta_{1}, B epsilon Delta_{2}$

$Rightarrow overrightarrow{AB} , . , overrightarrow{u_{1}} = 0$ hoặc $Rightarrow overrightarrow{AB} , . , overrightarrow{u_{2}} = 0$

$Rightarrow d(Delta_{1}, Delta_{2})=AB$

2. Các dạng bài tập về viết phương trình đường thẳng trong không gian và cách giải

2.1. Dạng 1: Viết phương trình đường thẳng bằng cách xác định vectơ chỉ phương

Xem thêm : Khi thủy phân saccarozơ thì thu được?

Ví dụ 1: Với tọa độ Oxyz trong không gian cho đường thẳng

d: $frac{x + 1}{2}=frac{y – 1}{1}=frac{z – 2}{3}$ và mặt phẳng P: $x-y-z-1=0$. Viết phương trình đường thẳng $Delta$ vuông góc với d, song song với (P) và đi qua A(1; 1; -2).

Giải:

Để tìm được vectơ chỉ phương của $Delta$ ta phải tìm 2 vectơ chỉ phương không cùng phương của nó sau đó tìm tích có hướng của 2 vecto.

Như vậy ta có: $overrightarrow{u_{Delta}}=[overrightarrow{u_{d}}; overrightarrow{_{p}}]=(2; 5; -3)$

Trong đó: $overrightarrow{u_{d}} = (2; 1; 3); overrightarrow{_{p}}=(1; -1; -1)$

$Delta$ đi qua A(1; 1; -2) và có vectơ chỉ phương $overrightarrow{u_{Delta}} = (2; 5; -3)$

$Rightarrow$ Ta có phương trình: $Delta : frac{x – 1}{2} = frac{y – 1}{5} = frac{z + 2}{-3}$

Ví dụ 2: Cho tọa độ Oxyz trong không gian cho đường thẳng

$Delta: frac{x – 1}{2} = frac{y + 1}{1} = frac{z}{-1}$ và mặt phẳng P: $x-y-z-1=0$. Viết phương trình đường thẳng d vuông góc và cắt với $Delta$, qua M(2; 1; 0).

Giải:

2.2. Dạng 2: Viết phương trình đường thẳng liên quan đến một đường thẳng khác

Ví dụ 1: Cho tọa độ Oxyz trong không gian cho đường thẳng

$d: frac{x + 1}{3}=frac{y – 2}{-2}=frac{z – 2}{2}$ và $P: x + 3y + 2z + 2=0$. Viết phương trình của $Delta$ song song với (P), cắt đường thẳng (d) và đi qua M(2; 2; 4).

Giải:

Ví dụ 2: Cho hệ tọa độ Oxyz trong không gian có đường thẳng $d: frac{x – 1}{2}=frac{y + 1}{1}=frac{z}{-1}$. Viết phương trình đường thẳng $Delta$ đi qua A(2; 3; -1) và cắt d tại B sao cho khoảng cách từ B đến $alpha: x + y + z = 0$ bằng $2sqrt{3}$.

Giải:

Do $B epsilon d Rightarrow$ Tọa độ B(1 + t; 2 + 2t; -t)

Do khoảng cách từ B tới $alpha: x + y + z = 0$ bằng $2sqrt{3}$ nên:

• Với t = 2 thì B(3; 6; -2)

$Delta$ đi qua B(3; 6; -2) và nhận $overrightarrow{AB} (1; 3; -1)$ làm vecto chỉ phương:

$Rightarrow$ Phương trình $Delta: frac{x – 3}{1}=frac{y – 6}{3}=frac{z – 2}{-1}$

• Với t = -4 thì B(-3; -6; 4)

Xem thêm : Top #26 Quán cafe Quận 2 TPHCM check – in sang chảnh

$Delta$ đi qua B(-3; -6; 4) và nhận $overrightarrow{AB}(-5; -9; 5)$ làm vecto chỉ phương:

$Rightarrow$ Phương trình $Delta: frac{x + 3}{-5}=frac{y + 6}{9}=frac{z – 4}{5}$

2.3. Dạng 3: Viết phương trình đường thẳng liên quan đến hai đường thẳng khác

Ví dụ 1: Cho hệ tọa độ Oxyz trong không gian, viết phương trình của đường thẳng d đi qua điểm M(-4; -5; 3) và cắt cả 2 đường thẳng $d_{1}: 2x + 3x + 11 = 0$ hoặc $y – 2z + 7 = 0$ và $d_{2}: frac{x – 2}{2}=frac{y + 1}{3}=frac{z – 1}{-5}$

Giải:

Viết phương trình đường thẳng:

Ví dụ 2: Cho hệ tọa độ Oxyz trong không gian với 3 đường thẳng có phương trình:

Viết phương trình đường thẳng $Delta$ biết $Delta$ cắt $d_{1}; d_{2}; d_{3}$ lần lượt tại A, B, C để AB = BC.

Giải:

Xét 3 điểm A, B, C lần lượt nằm trên $d_{1}; d_{2}; d_{3}$

Giả sử: A(t; 4 – t; -1 + 2t); B(u; 3 – 3u, -3u) và C(-1 + 5v, 1 + 2v, -1 + v)

Ta có A, B, C thẳng hàng và BC = AB ⇔ B chính là trung điểm của BC

Tọa độ 3 điểm A(1; 3; 1); B(0; 2; 0); C(-1; 1; -1)

$Delta$ đi qua B(0; 2; 0) và có $overrightarrow{CB}(1; 1; 1)$

Tham khảo ngay bộ tài liệu tổng hợp trọn bộ kiến thức và phương pháp giải mọi dạng bài tập trong đề thi THPT Quốc gia môn Toán

2.4. Dạng 4: Viết phương trình đường thẳng liên quan đến khoảng cách

Ví dụ 1: Cho tọa độ Oxyz trong không gian, đường thẳng $d: x = 2 + 4t; y = 3 = 2t$ và $z = -3 + t$. Mặt phẳng $(P): -x + y + 2z + 5 = 0$. Viết phương trình nằm trong mặt phẳng (P) song song và cách d một khoảng bằng $sqrt{14}$.

Giải:

Ví dụ 2:

Giải:

Đăng ký ngay để được các thầy cô tư vấn và xây dựng lộ trình ôn thi sớm hiệu quả và phù hợp nhất với bản thân

Trên đây là toàn bộ kiến thức lý thuyết và bài tập về phương trình đường thẳng trong không gian. Hy vọng rằng qua bài viết này các em có thể tự tin khi làm bài tập phần này. Để học nhiều hơn kiến thức về toán học lớp 12, truy cập trang web Vuihoc.vn ngay nhé!

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp