TỨ DIỆN ĐỀU – Công thức tính thể tích tứ diện đều cạnh a

Trong chương trình toán hình học lớp 12 và nội dung của kỳ thi THPT Quốc Gia. Thì các kiến thức về khối đa diện là rất quan trọng và chiếm một phần kiến thức rất lớn.

Trong phạm trù kiến thức về khối đa diện thì việc tính thể tích tứ diện đều là một nội dung không thể nào bỏ qua. Hiểu được tầm quan trọng của nó, ngay sau đây ITQNU xin được chia sẻ đến các bạn học sinh những kiến thức về tứ diện đều. Cũng như các cách tính thể tích tứ diện đều một cách chính xác nhất.

Bạn đang xem: TỨ DIỆN ĐỀU – Công thức tính thể tích tứ diện đều cạnh a

Khái niệm về tứ diện và tứ diện đều

Đầu tiên chúng ta sẽ phân ra 2 định nghĩa riêng biệt. Bao gồm khái niệm về hình tứ diện và hình tứ diện đều. Do đó, để giúp các bạn có thể hiểu chính xác hơn. Thì chúng ta sẽ đi định nghĩa từng loại hình sau đây:

1. Tứ diện là gì?

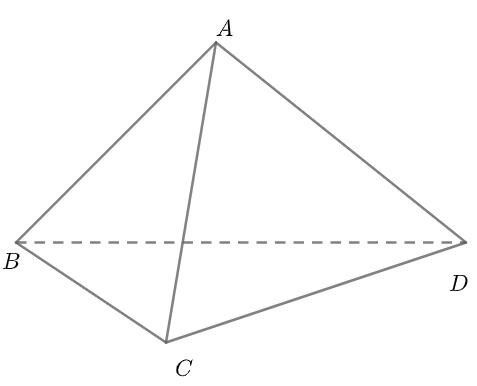
Hình tứ diện là hình có bốn đỉnh và thường được đặt với ký hiệu là A, B, C, D. Trong đó, với bất kỳ điểm nào trong số các điểm A, B, C, D cũng được xem là đỉnh của tứ diện. Mặt tam giác đối diện với đỉnh sẽ được gọi là mặt đáy. Ví dụ, nếu chọn B là đỉnh của tứ diện thì mặt đáy sẽ là (ACD).

Hay còn hiểu theo một cách gắn gọn khác thì trong không gian nếu cho 4 điểm không đồng phẳng gồm A, B, C, D. Thì khi đó khối đa diện có 4 đỉnh A, B, C, D gọi là khối tứ diện. Và được ký hiệu là ABCD.

2. Tứ diện đều là gì?

Nếu một hình tứ diện có các mặt bên là các tam giác đều thì đây được gọi là hình tứ diện đều. Và tứ diện đều được xem là một trong 5 khối đa diện đều.

Các tính chất của tứ diện đều

Tứ diện đều có các tính chất như sau:

• Bốn mặt xung quanh là các tam giác đều bằng nhau
• Các mặt của tứ diện là những tam giác có ba góc đều nhọn.
• Tổng các góc tại một đỉnh bất kì của tứ diện là 180.
• Hai cặp cạnh đối diện trong một tứ diện có độ dài bằng nhau
• Tất cả các mặt của tứ diện đều tương đương nhau.
• Bốn đường cao của tứ diện đều có độ dài bằng nhau.
• Tâm của các mặt cầu nội tiếp và ngoại tiếp nhau, trùng với tâm của tứ diện.
• Hình hộp ngoại tiếp tứ diện là hình hộp chữ nhật
• Các góc phẳng nhị diện ứng với mỗi cặp cạnh đối diện của tứ diện bằng nhau.
• Đoạn thẳng nối trung điểm của các cạnh đối diện là một đường thẳng đứng vuông góc của cả hai cạnh đó
• Một tứ diện có ba trục đối xứng
• Tổng các cos của các góc phẳng nhị diện chứa cùng một mặt của tứ diện bằng 1.

Cách vẽ hình tứ diện đều

Xem thêm :

Bất kỳ khi giải một bài toán liên quan tới hình tứ diện đều nào cũng vậy. Điều quan trọng nhất là chúng ta phải vẽ chính xác hình tứ diện đều. Từ đó chúng ta mới có một cái hình tổng thể và đưa ra các phương pháp giải chính xác nhất. Và sau đây sẽ là cách vẽ hình tứ diện đều chi tiết nhất:

• Bước 1: Đầu tiên các bạn hãy xem hình tứ diện đều là môt hình chóp tam giác đều A.BCD.
• Bước 2: Tiến hành vẽ mặt là cạnh đáy ví dụ là mặt BCD.
• Bước 3: Tiếp theo các bạn tiến hành vẽ một đường trung tuyến của mặt đáy BCD. Ví dụ đường trung tuyến này là BM.
• Bước 4: Sau đó các bạn tiến hành xác định trọng tâm G của tam giác BCD này. Khi đó G chính là tâm của đáy BCD.
• Bước 5: Tiến hành dựng đường cao .
• Bước 6: Xác định điểm A trên đường vừa dựng và hoàn thiện hình tứ diện đều.

Sau khi các bạn đã biết cách vẽ hình tứ diện đều rồi. Thì tiếp theo bài học chúng ta sẽ cùng nhau tìm hiểu về công thức tính thể tích tứ diện đều nhé.

Công thức tính thể tích tứ diện đều cạnh a

Một tứ diện đều sẽ có 6 cạnh bằng nhau và 4 mặt tam giác đều sẽ có các công thức tính thể tích như sau:

• Thể tích tứ diện ABCD: Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng: V = ⅓ x S (BCD) x AH
• Thể tích tứ diện đều tam giác S.ABC: Thể tích của một khối chóp bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp đó: V = ⅓ x B x h

Ví dụ minh họa

Tính thể tích khối tứ diện đều cạnh a.

Lời giả:

Giả sử ABCD là khối tứ diện đều cạnh a. G là trọng tâm tam giác BCD (hình trên).

Xem thêm : Bị nợ xấu vẫn vay được tiền từ ngân hàng: Có đúng không?

Cuối cùng tổng kết lại thì để tính thể tích tứ diện đều cạnh a. Thì ta sẽ có công thức sau đây:

Các dạng bài tập mẫu về tứ diện đều

Quy tắc tìm các mặt phẳng đối xứng. Trong tứ diện đều, do có tính chất đối xứng nhau. Do đó ta cứ đi từ trung điểm các cạnh ra mà tìm. Nếu bạn chọn một mặt phẳng đối xứng, hãy đảm bảo rằng các điểm còn lại được chia đều về hai phía

Ví dụ 1: tìm số mặt phẳng đối xứng của hình tứ diện đều.

Lời giải: Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện. Vì vậy, hình tứ diện đều sẽ có 6 mặt phẳng đối xứng.

Ví dụ 2: Cho hình chóp đều S.ABCD (đáy là hình vuông), đường SA vuông góc với mặt phẳng (ABCD). Xác định hình chóp này có mặt đối xứng nào.

Lời giải:

Ta có: BD vuông góc với AC, BD vuông góc với SA. Suy ra, BD vuông góc với (SAC). Từ đó ta suy ra (SAC) là mặt phẳng trung trực của BD. Ta kết luận rằng, (SAC) là mặt đối xứng của hình chóp và đây là mặt phẳng duy nhất.

Tổng kết

Như vậy, ITQNU vừa chia sẻ đến bạn kiến thức về tứ diện đều. Cũng như cách tính thể tích tứ diện đều. Trong chương trình toán hình học lớp 12 và nội dung của kỳ thi THPT Quốc Gia. Thì kiến thức về tứ diện đều là quan trọng. Hy vọng qua bài viết, các bạn học sinh có thêm nhiều kiến thức về tứ diện đều.

Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp