Công thức tính đường chéo hình vuông, đường chéo hình chữ nhật
Hiện nay nhiều bạn học sinh đang tìm công thức tính đường chéo hình chữ nhật, đường chéo hình vuông để áp dụng vào những bài tập, bài kiểm tra trong quá trình học. Đây là 2 công thức tính toán cơ bản trong hình học và các bạn cần tìm hiểu kỹ tính chất của hai đường chéo này thì mới học tập hiệu quả hơn. Bài viết sau sẽ chia sẻ 2 công thức tính đường chéo để các bạn cùng tìm hiểu chi tiết.
Trước khi tìm hiểu về đường chéo hình vuông thì bạn cần nắm tính chất của hình vuông. Hình vuông là dạng hình học mà mọi người có thể gặp ở bất cứ đâu trong đời sống. Hình vuông thường có điểm đặc trưng là bốn góc vuông và bốn cạnh có kích thước như nhau.
Bạn đang xem: Công thức tính đường chéo hình vuông, đường chéo hình chữ nhật
Bên cạnh đó, hình vuông có những tính chất như sau:
Dựa vào tính chất ở trên thì đường chéo trong hình vuông chính là một đoạn nối 2 đỉnh đối xứng trong hình vuông. Điểm đặc biệt là đường chéo này sẽ chia hình vuông ra 2 hình tam giác vừa vuông vừa cân và nằm đối nhau. Việc này có lợi khi bạn muốn tính kích thước của đường chéo và không nắm độ dài của các cạnh.
Như vậy thì đường chéo của hình vuông được coi như cạnh huyền thuộc hai tam giác có tính chất vuông cân. Vì vậy công thức để tính toán độ dài đường chéo hình vuông sẽ được tìm ra từ định lý của Pitago về tam giác vuông.
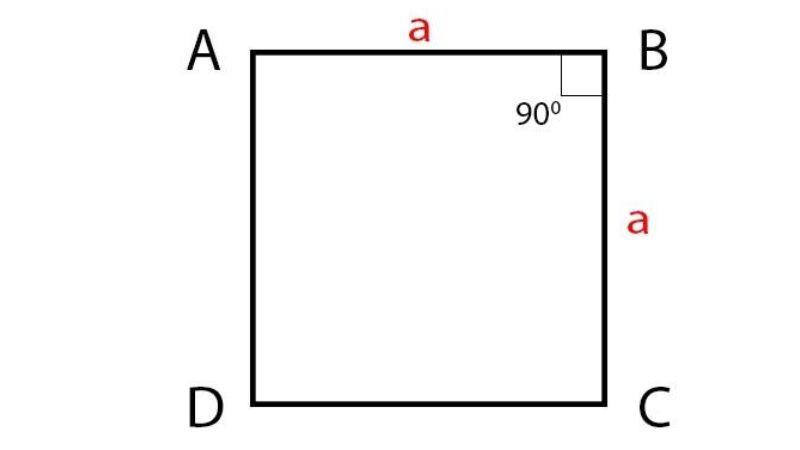
Ví dụ ta có một hình vuông tên là ABCD với độ dài các cạnh được gọi là a. Đường chéo là AC sẽ phân chia hình vuông này ra hai tam giác có tính chất vuông cân là tam giác ACD và tam giác ABC.
Khi áp dụng định lý của Pitago về tam giác có tính chất vuông cân ABC thì ta được:
Vì vậy ta có công thức tính đường chéo của hình vuông gồm độ dài các cạnh là a: AC (đường chéo) = a (cạnh hình vuông) x căn bậc hai của 2.
Bài tập 1: Giả sử ta có hình vuông có độ dài các cạnh là 3cm. Vậy độ dài đường chéo trong hình vuông này là bao nhiêu? √18cm hay 6cm, 5cm, 4cm?
Đáp án:
Ta có thể áp dụng định lý của Pitago cho hình vuông trên như sau:
AC² = AB² + BC²
= 3² + 3² = 18
Như vậy ta có thể suy ra được đường chéo của hình vuông trên có độ dài là AC = √18cm.
Bài tập 2: Cho 1 hình vuông có độ dài đường chéo là 2cm. Vậy các cạnh thuộc hình vuông này bằng bao nhiêu? 3/2 cm hay 1cm, √2cm, 4/3 cm?
Đáp án:
Chúng ta cũng áp dụng định lý của Pitago cho tam giác có tính chất vuông cân ABC. Bài tập trên đã có sẵn độ dài của đường chéo là 2cm nên ta có cạnh huyền AC = 2cm. Bây giờ chúng ta sẽ tìm độ dài của cạnh AB theo công thức sau:
AC² = AB² + BC²
= 2AB (BC = AB)
Từ đó suy ra:
AB² = AC² : 2
= 2² : 2 = 2
Như vậy thì AB có độ dài là √2.
Hiện nay việc tìm hiểu cách tính toán đường chéo trong hình vuông có thể ứng dụng vào nhiều lĩnh vực trong đời sống chúng ta như sau:
Xem thêm : Very Peri – Màu của hy vọng
Trong lĩnh vực thiết kế và xây dựng thì người ta áp dụng các tính toán đường chéo của hình vuông nhằm xác định được vị trí và kích thước của những nhân tố như cửa ra vào, cửa sổ, cách bài trí các đồ dùng nội thất cùng những chi tiết liên quan đến kiến trúc,…
Khi bạn muốn cắt hình vuông cho ra 2 phần như nhau hoặc muốn cắt 1 góc chuẩn thì công thức tính đường chéo trong hình vuông là rất hữu dụng để đem lại độ đẹp và chính xác.
Trong lĩnh vực đo đạc thì việc tính toán đường chéo hình vuông được áp dụng để tính khoảng cách kể từ 1 điểm tới 1 điểm khác qua 1 vị trí mà bạn không được tiếp cận một cách trực tiếp.
Trong lĩnh vực này thì công thức tính toán đường chéo trong hình vuông dùng để tính kích cỡ hiển thị của màn hình và kích thước của viền màn hình.
Lĩnh vực này cần áp dụng các tính toán đường chéo trong hình vuông để tính khoảng cách của tọa độ, diện tích những hình vuông tồn tại trong không gian 3D hoặc 2D.
Trong thiết kế đồ họa và nghệ thuật thì việc tính toán đường chéo của hình vuông được áp dụng để thiết lập sự đối xứng, cân đối trong những thiết kế đồ họa và những tác phẩm nghệ thuật.
Trong lĩnh vực này thì việc tính toán độ dài đường chéo trong hình vuông được ứng dụng nhằm xác định được góc với hình dạng những đối tượng có trong các hình ảnh.
Việc tính toán đường chéo hình vuông chính là định nghĩa hình học căn bản, nó có vai trò rất quan trọng ở những bài tính toán có liên quan về hình vuông và những dạng hình học tương tự.
Hình học chữ nhật được coi như dạng hình học tứ giác có tính lồi và bao gồm 4 góc đều vuông. Đường chéo trong hình này có vài tính chất đặc biệt và rất có ích khi giải những bài tập về hình học như sau:
Tương tự cách tính đường chéo hình vuông ở trên, từ những tính chất đường chéo của hình học chữ nhật được đề cập ở phần trên thì chúng ta hãy dùng định lý của Pitago vào tính độ dài của đường chéo trong hình chữ nhật như sau:
Ví dụ cho hình học chữ nhật là ABCD bao gồm chiều rộng với độ dài là b, chiều dài với độ dài là a và đường chéo là AC giống hình sau:
Khi dùng định lý của Pitago vào tam giác có góc vuông là ABC thì ta có:
Như vậy ta có kích thước đường chéo của hình học chữ nhật là căn bậc 2 của tổng 2 cạnh bình phương (chiều rộng và chiều dài) trong hình học chữ nhật:
Tương tự cách tính đường chéo hình vuông ở trên, các bạn học sinh có thể tham khảo một vài bài tập tính toán đường chéo hình chữ nhật như sau:
Hãy tìm ra độ dài của đường chéo trong hình học chữ nhật với chiều rộng là 5dm, chiều dài là 10dm.
Đáp án:
Ta gọi đường chéo có độ dài là a (điều kiện là a > 0 và đo lường bằng đơn vị là dm).
Theo định lý của Pitago thì đường chéo có độ dài là: a2 = 102 + 52. Vậy bình phương cạnh a bằng 125.
Như vậy độ dài đường chéo a bằng 5√5 dm.
Hãy tính ra độ dài của đường chéo trong hình học chữ nhật khi biết chiều rộng của hình là 5dm và chiều dài của hình là 10dm.
Đáp án:
Ta coi đường chéo trong hình trên có độ dài là a (với điều kiện là a > 0 và a có đơn vị là dm).
Chúng ta sẽ dùng định lý của Pitago để tính đường chéo như sau:
Xem thêm : Các quy phạm pháp luật bắt nguồn từ?
Một hình học chữ nhật có độ dài đường chéo là 13m và chiều dài của hình học chữ nhật lớn hơn độ dài chiều rộng của hình là 7m. Vậy hãy tính diện tích và chu vi của hình này.
Đáp án:
Ta gọi độ dài chiều rộng của hình là a (điều kiện là a > 0 và đơn vị là m). Suy ra ta có chiều dài bằng a + 7 (m).
Vì độ dài đường chéo trong hình trên là 13m nên ta sẽ dùng định lý của Pitago như sau:
Như vậy ta có độ dài chiều rộng là 5m cùng với chiều dài là 12m.
Suy ra ta có chu vi hình học chữ nhật bằng (5 + 12).2 = 34m và diện tích hình là 12 x 5 = 60m2.
Cho chu vi của 1 hình học chữ nhật là 28cm và 2 cạnh trong hình này hơn kém nhau khoảng 2cm. Vậy hãy tính toán độ dài đường chéo trong hình này.
Đáp án:
Ta có chiều rộng là a (với điều kiện a > 0 và đơn vị là m).
Suy ra ta có chiều dài bằng a + 2 (m).
Như vậy chu vi của hình là 28cm nên suy ra: (a + a + 2).2 = 28.
Suy ra a = 6 (điều kiện đặt ra được thỏa mãn).
Như vậy thì hình học chữ nhật có chiều rộng bằng 6m với chiều dài trong hình bằng 8m.
Gọi đường chéo của hình trên có độ dài là d thì chúng ta dùng định lý Pitago để tính toán như sau:
Cho chu vi của 1 hình học chữ nhật là 32m với diện tích của hình này là 60m2. Hãy tính toán đường chéo trong hình này có độ dài bao nhiêu?
Đáp án:
Ta có ½ chu vi của hình trên là 32/2 = 16 (m).
Ta gọi chiều rộng hình bằng a (với điều kiện 0 < a < 16 và đơn vị là m).
Như vậy chiều dài bằng 16 – a (m).
Vì diện tích hình trên là 60m2 nên suy ra:
Ta gọi đường chéo trong hình học chữ nhật này có độ dài là d thì ta có:
Nội dung bài viết đã chia sẻ về công thức tính đường chéo hình vuông và đường chéo hình chữ nhật cho mọi người tham khảo. Các bạn học sinh muốn học tốt môn toán hình thì phải nắm vững 2 công thức trên vì nó có thể giúp bạn xử lý nhiều bài tập trong quá trình học.
Tham khảo bài viết liên quan:
Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp
This post was last modified on 10/02/2024 23:44
Con số may mắn hôm nay 23/11/2024 theo năm sinh: Nhặt TIỀN từ con số…
Tử vi thứ bảy ngày 23/11/2024 của 12 con giáp: Tuổi Thìn chán nản, tuổi…
Vận may của 4 con giáp đang ngày càng xuống dốc. Cuối tuần này (23-24/11),…
Con số cuối cùng trong ngày sinh dự đoán con người sẽ GIÀU CÓ, sống…
Cuối tuần này (23-24/11), 4 con giáp sẽ gặp nhiều may mắn và thành công…
Tử vi hôm nay – Top 3 con giáp thịnh vượng nhất ngày 22/11/2024