Tính đường cao trong tam giác là một loại bài tập phổ biến trong học toán, liên quan đến việc tính diện tích tam giác. Nếu bạn cần biết về công thức tính đường cao tam giác, hãy tham khảo bài viết về cách tính đường cao trong tam giác cân, đều và vuông dưới đây.
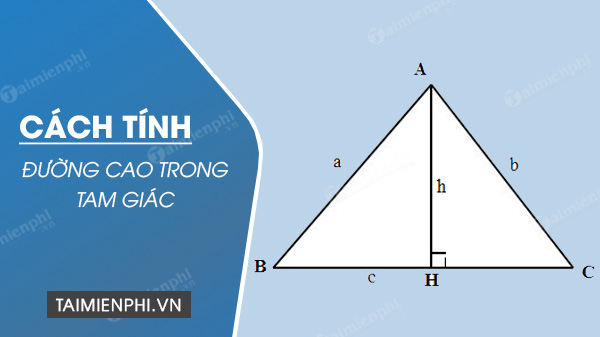
Cách tính đường cao trong tam giác vuông, tam giác đều và tam giác cân
I. Phương trình tính đường cao trong tam giác
1. Trường hợp 1: Tam giác tự nhiên
Phương trình tính chiều cao của tam giác:
Trong đó:- a, b, c là độ dài các cạnh của tam giác.- h là chiều cao của tam giác.- p là nửa chu vi của tam giác, có công thức p = (a + b + c) : 2.
2. Tình huống 2: Tam giác cân
Cho tam giác ABC có hai cạnh bằng nhau tại đỉnh A và đường cao AH là đường vuông góc với cạnh AB.
Vì tam giác ABC cân tại A, nên AH cũng là đường trung tuyến, nên có: HB = HC = BC/2.
Xem thêm : Nêu cấu tạo roto của động cơ không đồng bộ 3 pha?
Áp dụng định lý Pythagoras cho tam giác vuông AHB tại H, ta có:
Để tính đường cao trong tam giác đều, chúng ta cần áp dụng một số công thức đặc biệt.
4. Câu chuyện về tam giác vuông
Trong tam giác vuông ABC, chúng ta có thể áp dụng các quy tắc hữu ích sau:
II. Ví dụ thực hành về tính đường cao trong tam giác
Ví dụ 1: Trong tam giác ABC vuông tại A, với AB : AC = 3 : 4 và AB + AC = 21cm. Tính các cạnh và đường cao AH.
Giải
Áp dụng phương pháp tính đường cao trong tam giác vuông để giải bài toán.
Ví dụ 2: Tính đường cao AH và diện tích tam giác ABC với AB = 4 cm, BC = 7 cm, AC = 5 cm.
Giải:
Khi tính đường cao trong tam giác, bạn có thể dễ dàng tính diện tích và độ dài các cạnh của tam giác.
Tam giác đều là một trường hợp đặc biệt của tam giác, và cách tính đường cao trong tam giác đều dựa vào công thức cụ thể.
Nguồn: https://luatduonggia.edu.vn
Danh mục: Tổng hợp